题目内容
13.$\sqrt{10}$的整数部分是x,小数部分是y,则y(x+$\sqrt{10}$)的值为1.分析 由于3<$\sqrt{10}$<4,由此可确定$\sqrt{10}$的整数部分x=3,接着确定小数部分y=$\sqrt{10}$-3,然后代入所求代数式中恰好利用平方差公式计算出结果.
解答 解:∵3<$\sqrt{10}$<4,
∴$\sqrt{10}$的整数部分x=3,小数部分y=$\sqrt{10}$-3,
∴y(x+$\sqrt{10}$)=($\sqrt{10}$-3)(3+$\sqrt{10}$)=($\sqrt{10}$)2-32=10-9=1.
故答案为:1.
点评 此题考查了二次根式的性质,首先利用二次根式的性质确定x、y的值,然后在代数式中利用平方差公式化简计算即可解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.如果要证明平行四边形ABCD为正方形,那么我们需要在四边形ABCD是平行四边形的基础上,进一步证明( )
| A. | AC和BD互相垂直平分 | B. | AB=AD且AC⊥BD | ||
| C. | ∠A=∠B且AC=BD | D. | AB=AD且AC=BD |
8.某超市电器销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
(1)求A、B两种型号的电风扇的销售价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能请给出采购方案.若不能,请说明理由.
| 销售时段 | 销售量 | 销售收入 | |
| A型号 | B型号 | ||
| 第一周 | 3台 | 5台 | 1800元 |
| 第二周 | 4台 | 10台 | 3100元 |
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能请给出采购方案.若不能,请说明理由.
18.在下列说法中:①10的平方根是±$\sqrt{10}$;②-2是4的一个平方根;③$\frac{4}{9}$的平方根是$\frac{2}{3}$;④0.01的算术平方根是0.1;⑤$\sqrt{(-2)^{2}}$=2,正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
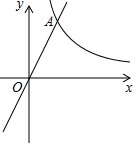 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{8}{x}$的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{8}{x}$的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C. 我区某校数学学习小组利用所学的三角函数知识测量我区某座山的高度.如图,他们在山脚下的B处测得山顶C的仰角是45°,从B处沿坡度为1:$\sqrt{3}$的斜坡前进100米到达山腰的一个观景点D,在点D处再次测得山顶C的仰角为60°,则该座山的高度AC为( )(注:结果精确到1米,参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
我区某校数学学习小组利用所学的三角函数知识测量我区某座山的高度.如图,他们在山脚下的B处测得山顶C的仰角是45°,从B处沿坡度为1:$\sqrt{3}$的斜坡前进100米到达山腰的一个观景点D,在点D处再次测得山顶C的仰角为60°,则该座山的高度AC为( )(注:结果精确到1米,参考数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)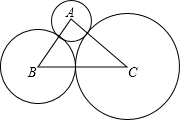 如图,⊙A、⊙B、⊙C两两外切,AB=10,BC=21,sinB=$\frac{4}{5}$.
如图,⊙A、⊙B、⊙C两两外切,AB=10,BC=21,sinB=$\frac{4}{5}$.