题目内容
 如图,在平面直角坐标系xOy中,点A的坐标为(1,
如图,在平面直角坐标系xOy中,点A的坐标为(1,| 3 |
| k |
| x |
考点:反比例函数综合题
专题:综合题
分析:作EH⊥x轴于H,先得到OB=1,AB=
,则利用勾股定理计算出OA=2,根据含30度的直角三角形三边的关系得∠A=30°,∠AOB=60°;设F点坐标为(1,a),则AF=
-a,在Rt△AEF中可得到EF=
AF=
,AE=
EF=
,所以OE=AO-AE=
,在Rt△OEH中,根据含30度的直角三角形三边的关系得OH=
OE=
,EH=
OH=
,则E点坐标为(
,
),然后根据反比例函数图象上点的坐标特征得1•a=
•
,解此方程得到得a1=
,a2=
(舍去),由此得到E点坐标为(
,
),F点坐标为(1,
),最后利用待定系数法确定直线EF的解析式.
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
3-
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| 3 |
3a+
| ||
| 4 |
| ||
| 4 |
3a+
| ||
| 4 |
| ||
| 4 |
3a+
| ||
| 4 |
| ||
| 9 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
| ||
| 9 |
解答: 解:作EH⊥x轴于H,如图,
解:作EH⊥x轴于H,如图,
∵点A的坐标为(1,
),
∴OB=1,AB=
,
而AB⊥x轴,
∴OA=
=2,
∴∠A=30°,∠AOB=60°,
设F点坐标为(1,a),则AF=
-a,
在Rt△AEF中,∠A=30°,
∴EF=
AF=
,
∴AE=
EF=
,
∴OE=AO-AE=
,
在Rt△OEH中,∠OEH=30°,
∴OH=
OE=
,
∴EH=
OH=
,
∴E点坐标为(
,
),
∵点E、F都在y=
的图象上,
∴1•a=
•
,
整理得3
a2-10a+
=0,解得a1=
,a2=
(舍去),
∴E点坐标为(
,
),F点坐标为(1,
),
设直线EF的解析式为y=mx+n,
把E(
,
),F(1,
)代入得
,解得
,
所以直线EF的解析式为y=-
x+
.
 解:作EH⊥x轴于H,如图,
解:作EH⊥x轴于H,如图,∵点A的坐标为(1,
| 3 |
∴OB=1,AB=
| 3 |
而AB⊥x轴,
∴OA=
| OB2+AB2 |
∴∠A=30°,∠AOB=60°,
设F点坐标为(1,a),则AF=
| 3 |
在Rt△AEF中,∠A=30°,
∴EF=
| 1 |
| 2 |
| ||
| 2 |
∴AE=
| 3 |
3-
| ||
| 2 |
∴OE=AO-AE=
| ||
| 2 |
在Rt△OEH中,∠OEH=30°,
∴OH=
| 1 |
| 2 |
| ||
| 4 |
∴EH=
| 3 |
3a+
| ||
| 4 |
∴E点坐标为(
| ||
| 4 |
3a+
| ||
| 4 |
∵点E、F都在y=
| k |
| x |
∴1•a=
| ||
| 4 |
3a+
| ||
| 4 |
整理得3
| 3 |
| 3 |
| ||
| 9 |
| 3 |
∴E点坐标为(
| 1 |
| 3 |
| ||
| 3 |
| ||
| 9 |
设直线EF的解析式为y=mx+n,
把E(
| 1 |
| 3 |
| ||
| 3 |
| ||
| 9 |
|
|
所以直线EF的解析式为y=-
| ||
| 3 |
4
| ||
| 9 |
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征和含30度的直角三角形三边的关系;会运用因式分解法解一元二次方程和利用待定系数法确定一次函数的解析式.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
四个数-
,0,3.14,
中,为无理数的是( )
| 1 |
| 2 |
| 3 |
A、-
| ||
| B、0 | ||
| C、3.14 | ||
D、
|
 已知抛物线y=ax2-2ax-4与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.
已知抛物线y=ax2-2ax-4与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.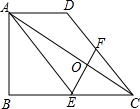 已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E是BC的中点、F是CD上的点,联结AE、EF、AC.
已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E是BC的中点、F是CD上的点,联结AE、EF、AC.
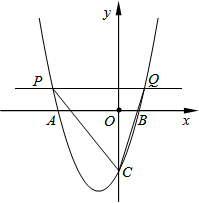 如图,在平面直角坐标系xOy中,二次函数y=ax2+bx-3(a,b是常数)的图象与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.
如图,在平面直角坐标系xOy中,二次函数y=ax2+bx-3(a,b是常数)的图象与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.