题目内容
 已知抛物线y=ax2-2ax-4与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.
已知抛物线y=ax2-2ax-4与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.(1)求抛物线的对称轴及表达式;
(2)若点P在x轴上方的抛物线上,且tan∠PAB=
| 1 |
| 2 |
(3)在(2)的条件下,过C作射线交线段AP于点E,使得tan∠BCE=
| 1 |
| 2 |
考点:二次函数综合题
专题:
分析:(1)根据对称轴直线公式求得对称轴;由抛物线解析式求得点C的坐标,然后由三角形面积公式来求a的值;
(2)如图,过P作PH⊥x轴于点H.根据已知条件可设PH=k,AH=2k,则P点的坐标是(2k-2,k)(k>0).根据二次函数图象上点的坐标特征得到:k=
(2k-2)2-(2k-2)-4,则易求k的值;
(3)是.设AE交y轴于点D,通过证明△AOC∽△EBC,推知对应角相等:∠EBC=∠AOC=90°,故BE⊥BC.
(2)如图,过P作PH⊥x轴于点H.根据已知条件可设PH=k,AH=2k,则P点的坐标是(2k-2,k)(k>0).根据二次函数图象上点的坐标特征得到:k=
| 1 |
| 2 |
(3)是.设AE交y轴于点D,通过证明△AOC∽△EBC,推知对应角相等:∠EBC=∠AOC=90°,故BE⊥BC.
解答:(1)解:∵抛物线y=ax2-2ax-4,
∴与y轴交点C(0,-4)
∴对称轴为直线x=
=1,
∵抛物线与x轴交于点A、B,且△ABC的面积为12,∴AB=6,
∴点A(-2,0),B(4,0),
∵抛物线过点A,
∴0=4a+4a-4,∴a=
,
∴抛物线表达式为y=
x2-x-4;
(2)解:如图,过P作PH⊥x轴于点H.
∵tan∠PAB=
,
∴设PH=k,AH=2k,
∴P点的坐标是(2k-2,k)(k>0).
∵点P在抛物线上,
∴k=
(2k-2)2-(2k-2)-4,
∴k=
,
∴P(5,
);
(3)是.
证明:设AE交y轴于点D,
∵A(-2,0),C(0,-4),
∴tan∠ACO=
,
∵tan∠PAB=
,
∴∠PAB=∠ACO,
∵∠ACO+∠OAC=90°,
∴∠PAB+∠OAC=90°,
∴PA⊥AC,
∵tan∠BCE=
,
∴∠ACO=∠BCE,
∴∠ACE=∠OCB
∵B(4,0),C(0,-4),
∴∠OCB=45°,∠ACE=45°,
∵A(-2,0),C(0,-4),
∴AO=2,OC=4,
∴AC=2
,
∴CE=2
,
∵B(4,0),C(0,-4),
∴BC=4
在△AOC和△EBC中,
=
=
,
=
=
,
∴
=
,
又∠ACO=∠BCE,
∴△AOC∽△EBC,
∴∠EBC=∠AOC=90°,
∴BE⊥BC.
∴与y轴交点C(0,-4)
∴对称轴为直线x=
| 2a |
| 2a |
∵抛物线与x轴交于点A、B,且△ABC的面积为12,∴AB=6,
∴点A(-2,0),B(4,0),
∵抛物线过点A,
∴0=4a+4a-4,∴a=
| 1 |
| 2 |
∴抛物线表达式为y=
| 1 |
| 2 |
(2)解:如图,过P作PH⊥x轴于点H.
∵tan∠PAB=
| 1 |
| 2 |

∴设PH=k,AH=2k,
∴P点的坐标是(2k-2,k)(k>0).
∵点P在抛物线上,
∴k=
| 1 |
| 2 |
∴k=
| 7 |
| 2 |
∴P(5,
| 7 |
| 2 |
(3)是.
证明:设AE交y轴于点D,
∵A(-2,0),C(0,-4),
∴tan∠ACO=
| 1 |
| 2 |
∵tan∠PAB=
| 1 |
| 2 |
∴∠PAB=∠ACO,
∵∠ACO+∠OAC=90°,
∴∠PAB+∠OAC=90°,
∴PA⊥AC,
∵tan∠BCE=
| 1 |
| 2 |
∴∠ACO=∠BCE,
∴∠ACE=∠OCB
∵B(4,0),C(0,-4),
∴∠OCB=45°,∠ACE=45°,
∵A(-2,0),C(0,-4),
∴AO=2,OC=4,
∴AC=2
| 5 |
∴CE=2
| 10 |
∵B(4,0),C(0,-4),
∴BC=4
| 2 |
在△AOC和△EBC中,
| AC |
| OC |
2
| ||
| 4 |
| ||
| 2 |
| CE |
| CB |
2
| ||
4
|
| ||
| 2 |
∴
| AC |
| OC |
| CE |
| CB |
又∠ACO=∠BCE,
∴△AOC∽△EBC,
∴∠EBC=∠AOC=90°,
∴BE⊥BC.
点评:本题综合考查了待定系数法求二次函数解析式,二次函数图象上点的坐标特征,相似三角形的判定与性质以及点的坐标与图形性质.综合性强,能力要求极高.考查学生数形结合的数学思想方法.

练习册系列答案
相关题目
计算(-2a3b)2的结果是( )
| A、-2a6b |
| B、4a6b2 |
| C、-4a6b2 |
| D、4a5b2 |
下列图案中,是中心对称又是轴对称的图形是( )
A、 |
B、 |
C、 |
D、 |
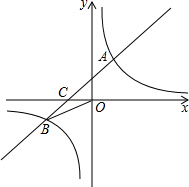 已知:如图,在平面直角坐标系中,一次函数y=ax+b (a≠0)的图象与反比例函数y=
已知:如图,在平面直角坐标系中,一次函数y=ax+b (a≠0)的图象与反比例函数y= 在某水果店一次性购买A种水果的单价y(元)与购买量x(千克)的函数关系如图.
在某水果店一次性购买A种水果的单价y(元)与购买量x(千克)的函数关系如图. 如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=
如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=
 如图,在平面直角坐标系xOy中,点A的坐标为(1,
如图,在平面直角坐标系xOy中,点A的坐标为(1, 如图,在平面直角坐标系中,点A、B分别在x轴、y轴的正半轴上,点B的坐标是(0,7),且AB=25.△AOB绕某点旋转180°后,点C(36,9)是点B的对应点.
如图,在平面直角坐标系中,点A、B分别在x轴、y轴的正半轴上,点B的坐标是(0,7),且AB=25.△AOB绕某点旋转180°后,点C(36,9)是点B的对应点.