题目内容
12.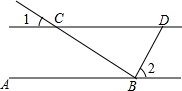 如图所示,AB∥CD,CB⊥DB,∠1=30°,则∠2=60°.
如图所示,AB∥CD,CB⊥DB,∠1=30°,则∠2=60°.
分析 根据平行线的性质求出∠CBA,求出∠CBD,即可求出答案.
解答 解:∵AB∥CD,∠1=30°,
∴∠CBA=∠1=30°,
∵CB⊥DB,
∴∠CBD=90°,
∴∠2=180°-∠CBD-∠CBA=60°,
故答案为:60°.
点评 本题考查了垂直定义,平行线的性质的应用,解此题的关键是求出∠CBA的度数,注意:两直线平行,内错角相等.

练习册系列答案
相关题目
3.某班有50名同学,期末考试优秀的学生人数及科目如表:
这里,一科优秀者包括两、三科优秀者,两科优秀者里也包括三科优秀者,试说明上述统计表的错误.
| 单科 | 两科 | 三科 | |||||
| 科目 | 数学 | 英语 | 语文 | 语文 数学 | 英语 数学 | 英语 语文 | 语文、数学、英语 |
| 人数 | 32 | 31 | 29 | 16 | 17 | 18 | 10 |
7.下列计算正确的是( )
| A. | 2t-t=2 | B. | t2•t3=t6 | C. | (-t2)3=-t5 | D. | t3÷t2=t |
2.-$\frac{2}{3}$的相反数是( )
| A. | -$\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |




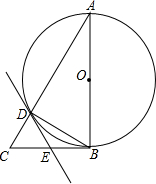 如图所示,△ABC中,∠ABC=90°,点O是AB的中点,以AB为直径作圆与AC交于点D,作∠BDE=∠A,DE与BC交于点E.
如图所示,△ABC中,∠ABC=90°,点O是AB的中点,以AB为直径作圆与AC交于点D,作∠BDE=∠A,DE与BC交于点E.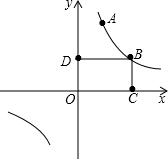 如图已知反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象上有不同的两点A和B,其中A(2,6),O是原点.过点B作BC⊥x轴于C,作BD⊥y轴于D,四边形OCBD的周长为14.
如图已知反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象上有不同的两点A和B,其中A(2,6),O是原点.过点B作BC⊥x轴于C,作BD⊥y轴于D,四边形OCBD的周长为14.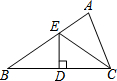 如图,在△ABC中,BC边的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为( )
如图,在△ABC中,BC边的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为( )