题目内容
17.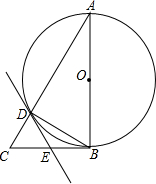 如图所示,△ABC中,∠ABC=90°,点O是AB的中点,以AB为直径作圆与AC交于点D,作∠BDE=∠A,DE与BC交于点E.
如图所示,△ABC中,∠ABC=90°,点O是AB的中点,以AB为直径作圆与AC交于点D,作∠BDE=∠A,DE与BC交于点E.(1)求证:DE是圆O的切线;
(2)求证:△BCD∽△ACB;
(3)若DE=mBC,写出m的值.
分析 (1)连结OD,如图,利用圆周角相等得∠ADB=90°,则∠A+∠ABD=90°,而∠BDE=∠A,∠OBD=∠ODB,所以∠BDE+∠ODB=90°,于是根据切线的判定定理得DE是圆O的切线;
(2)根据两个角对应相等的两个三角形相似进行判断;
(3)利用等角的余角相等得到∠BDE=∠CBD,∠C=∠CDE,则DE=BE,DE=CE,即DE=$\frac{1}{2}$BC,所以m=$\frac{1}{2}$.
解答 (1)证明:连结OD,如图,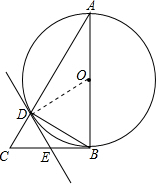
∵AB为直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
∵∠BDE=∠A,
∴∠BDE+∠ABD=90°,
∵OD=OB,
∴∠OBD=∠ODB,
∴∠BDE+∠ODB=90°,即∠ODE=90°,
∴OD⊥DE,
∴DE是圆O的切线;
(2)证明:∵∠BCD=∠ACB,∠BDC=∠ABC,
∴△BCD∽△ACB;
(3)解:∵∠CBD+∠ABD=90°,∠A+∠ABD=90°,
∴∠A=∠CBD,
而∠BDE=∠A,
∴∠BDE=∠CBD,
∴DE=BE,
∵∠C+∠A=90°,∠CDE+∠BDE=90°,
∴∠C=∠CDE,
∴DE=CE,
即DE=CE=BE,
∴DE=$\frac{1}{2}$BC,
∴m=$\frac{1}{2}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了相似三角形的判定与性质.

练习册系列答案
相关题目
5.函数y=$\sqrt{x}$中,自变量x的取值范围是( )
| A. | x>0 | B. | x<0 | C. | x≠0 | D. | x≥0 |
9.某校园足球队由13位男生组成,体育课上统计了所有男生所穿运动鞋的尺码,列表为:
则这13双运动鞋尺码的众数和中位数分别是( )
| 尺码(单位:码) | 38 | 39 | 40 | 41 | 42 |
| 数量(单位:双) | 2 | 5 | 3 | 1 | 2 |
| A. | 40码、39码 | B. | 39码、40码 | C. | 39码、39码 | D. | 40码、40码 |
7.在平面直角坐标系中,经过二、三、四象限的直线l过点(-2,-3).点(-1,a),(0,b),(c,1)都在直线l上,则下列判断正确的是( )
| A. | a<b | B. | c>-1 | C. | a>-3 | D. | c<-2 |
 如图,直线AB,CD被直线EF所截,∠1=∠2,AB∥CD吗?为什么?
如图,直线AB,CD被直线EF所截,∠1=∠2,AB∥CD吗?为什么? 已知:如图,在平面直角坐标系中,O为坐标原点,△OAB的顶点A、B的坐标分别是A(0,5),B(3,1),过点B画BC⊥AB交直线y=-m(m>$\frac{5}{4}$)于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.
已知:如图,在平面直角坐标系中,O为坐标原点,△OAB的顶点A、B的坐标分别是A(0,5),B(3,1),过点B画BC⊥AB交直线y=-m(m>$\frac{5}{4}$)于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.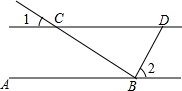 如图所示,AB∥CD,CB⊥DB,∠1=30°,则∠2=60°.
如图所示,AB∥CD,CB⊥DB,∠1=30°,则∠2=60°.