题目内容
16.先化简,再求值:($\frac{1}{a-b}-\frac{1}{a+b}$)$÷\frac{b}{{a}^{2}-2ab+{b}^{2}}$,其中a=$\sqrt{3}+\sqrt{2}$,b=$\sqrt{3}-\sqrt{2}$.分析 先根据分式混合运算的法则把原式进行化简,再把a、b的值代入进行计算即可.
解答 解:原式=$\frac{a+b-a+b}{(a-b)(a+b)}$•$\frac{(a-b)^{2}}{b}$
=$\frac{2b}{(a-b)(a+b)}$•$\frac{{(a-b)}^{2}}{b}$
=$\frac{2(a-b)}{a+b}$.
当a=$\sqrt{3}$+$\sqrt{2}$,b=$\sqrt{3}$-$\sqrt{2}$时,原式=$\frac{2(\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2})}{\sqrt{3}+\sqrt{2}+\sqrt{3}-\sqrt{2}}$=$\frac{2×2\sqrt{2}}{2\sqrt{3}}$=$\frac{2\sqrt{6}}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
11.张先生先到银行存了一笔三年的定期存款,年利率是4.25%,如果到期后取出的本息和为43825元,设张先生存入的本金为x元,则下面所列方程正确的是( )
| A. | x+3×4.25%x=43825 | B. | x+4.25%x=43825 | ||
| C. | 3×4.25%x=43825 | D. | 3(x+4.25%x)=43825 |
1.下列各数中,绝对值最大的实数是( )
| A. | π | B. | -2 | C. | $\frac{4}{3}$ | D. | -$\sqrt{7}$ |
6.已知:a2+a+1=5,则(2+a)(1-a)的值为( )
| A. | -4 | B. | -3 | C. | -2 | D. | 7 |
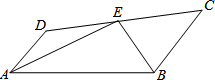 如图:E在线段CD上,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°.设AD=x,BC=y,且(x-3)2+|y-4|=0,AB的长度是( )
如图:E在线段CD上,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°.设AD=x,BC=y,且(x-3)2+|y-4|=0,AB的长度是( )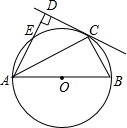 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E.
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E.