题目内容
6.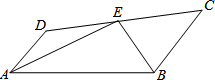 如图:E在线段CD上,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°.设AD=x,BC=y,且(x-3)2+|y-4|=0,AB的长度是( )
如图:E在线段CD上,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°.设AD=x,BC=y,且(x-3)2+|y-4|=0,AB的长度是( )| A. | 5 | B. | 6 | C. | 8 | D. | 7 |
分析 如图,过E作EF∥AD,交AB于F,根据绝对值和完全平方公式的性质得出x,y的值,根据已知得出∠EAB+∠EBA+∠DAE+∠EBC=90°+90°=180°,再由平行线的判定得出即可则∠DAE=∠AEF,∠EBC=∠BEF,因为EA、EB分别平分∠DAB和∠CBA,所以AF=EF=FB,再根据梯形中位线定理易求AB的长.
解答 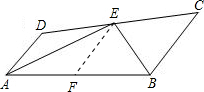 解:如图,过E作EF∥AD,交AB于F,
解:如图,过E作EF∥AD,交AB于F,
∵(x-3)2+|y-4|=0,
∴x-3=0,y-4=0,
解得:x=3,y=4,
∴AD=3,BC=4;
∵EA、EB分别平分∠DAB和∠CBA,
∴∠DAE=∠EAB,∠CBE=∠EBA,
∵∠AEB=90°,∴∠EAB+∠EBA=90°,
∴∠DAE+∠EBC=90°,
∴∠EAB+∠EBA+∠DAE+∠EBC=90°+90°=180°,
∴AD∥BC.∵AD∥BC,EF∥AD,
∴AD∥EF∥BC,
则∠DAE=∠AEF,∠EBC=∠BEF,
∵EA、EB分别平分∠DAB和∠CBA,
∴∠EAF=∠AEF,∠EBF=∠BEF,
∴AF=EF=FB,
又∵EF∥AD∥BC,
∴EF是梯形ABCD的中位线,
∴EF=$\frac{AD+BC}{2}$=$\frac{7}{2}$,
∴AB=7.
故选D.
点评 此题主要考查了平行线的判定和绝对值的性质等知识,根据已知得出∠DAE+∠EBC=90°是解题关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
17. 如图,在?ABCD中,AB=4,AD=2$\sqrt{2}$,E,F分别为边AB,CD上的点,若四边形AECF为正方形,则∠D的度数为( )
如图,在?ABCD中,AB=4,AD=2$\sqrt{2}$,E,F分别为边AB,CD上的点,若四边形AECF为正方形,则∠D的度数为( )
 如图,在?ABCD中,AB=4,AD=2$\sqrt{2}$,E,F分别为边AB,CD上的点,若四边形AECF为正方形,则∠D的度数为( )
如图,在?ABCD中,AB=4,AD=2$\sqrt{2}$,E,F分别为边AB,CD上的点,若四边形AECF为正方形,则∠D的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
11.正五边形的中心角等于( )
| A. | 18° | B. | 36° | C. | 54° | D. | 72° |
15.估计$\sqrt{7}$+2的值在( )
| A. | 2到3之间 | B. | 3到4之间 | C. | 4到5之间 | D. | 5到6之间 |
 如图,E,F是四边形ABCD的对角线BD上的两点,AB=CD,AD=CB,DF=BE.求证:AE∥CF.
如图,E,F是四边形ABCD的对角线BD上的两点,AB=CD,AD=CB,DF=BE.求证:AE∥CF.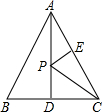 如图,在边长为2的等边△ABC中,AD是BC边上的高线,点E是AC中点,点P是AD上一动点,则PC+PE的最小值是$\sqrt{3}$.
如图,在边长为2的等边△ABC中,AD是BC边上的高线,点E是AC中点,点P是AD上一动点,则PC+PE的最小值是$\sqrt{3}$.