题目内容
5.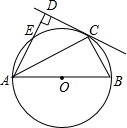 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E.
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E.(1)求证:AC平分∠DAB;
(2)若AD=6,CD=2$\sqrt{3}$,求⊙O的半径.
分析 (1)连接OC,由CD是⊙O的切线,AD⊥CD可以得到OC∥AD,然后可以推出∠1=∠2,又OC=OA,由等边对等角得∠1=∠3,所以∠2=∠3,即AC平分∠DAB;
(2)首先证明△ADC∽△ACB,求得AC的长,根据相似三角形对应边的比相等求解.
解答 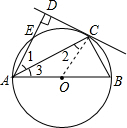 (1)证明:如右图所示,连接OC,
(1)证明:如右图所示,连接OC,
∵CD是⊙O的切线,
∴OC⊥CD;
又AD⊥CD,
∴OC∥AD,
∴∠1=∠2,
∵OC=OA,
∴∠1=∠3,
∴∠2=∠3,即AC平分∠DAB.
(2)解:∵AB是圆的直径,
∴∠ACB=90°.
∴∠ACB=∠ADC,
又∵∠1=∠3,
∴△ADC∽△ACB.
∴$\frac{AC}{AB}$=$\frac{AD}{AC}$.
∵直角△ADC中,∠ADC=90°,AD=6,CD=2$\sqrt{3}$,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{{6}^{2}+(2\sqrt{3})^{2}}$=4$\sqrt{3}$.
∴$\frac{4\sqrt{3}}{AB}$=$\frac{6}{4\sqrt{3}}$,
解得:AB=8.
∵AB是直径,
∴圆的半径是4.
点评 本题考查了切线的性质以及相似三角形的判定与性质,正确证明△ADC∽△ACB是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.估计$\sqrt{7}$+2的值在( )
| A. | 2到3之间 | B. | 3到4之间 | C. | 4到5之间 | D. | 5到6之间 |
20.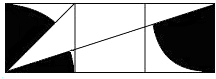 如图,方格纸中3个小正方形的边长均为1,则图中三个以1为半径的小扇形阴影部分的面积和为( )
如图,方格纸中3个小正方形的边长均为1,则图中三个以1为半径的小扇形阴影部分的面积和为( )
 如图,方格纸中3个小正方形的边长均为1,则图中三个以1为半径的小扇形阴影部分的面积和为( )
如图,方格纸中3个小正方形的边长均为1,则图中三个以1为半径的小扇形阴影部分的面积和为( )| A. | $\frac{1}{3}π$ | B. | $\frac{3}{8}π$ | C. | $\frac{1}{2}π$ | D. | $\frac{2}{3}π$ |
17.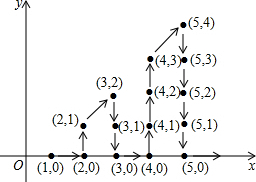 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…根据这个规律探索可得,第102个点的坐标为( )
如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…根据这个规律探索可得,第102个点的坐标为( )
 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…根据这个规律探索可得,第102个点的坐标为( )
如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…根据这个规律探索可得,第102个点的坐标为( )| A. | (13,8) | B. | (13,10) | C. | (14,8) | D. | (14,10) |

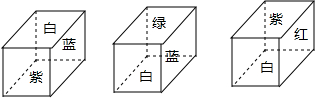 一个正方体的六个面上分别涂有红、白、黄、绿、蓝、紫六种不同的颜色,其中红、白、黄、绿、蓝、紫,分别代表的是数字-1、-2、-3、-4、-5、-6中的一个数,如图是这个正方体的三种放置方法,若三个正方体下底面所标颜色代表的数字分别是a,b,c,则a+b+c+abc=-85.
一个正方体的六个面上分别涂有红、白、黄、绿、蓝、紫六种不同的颜色,其中红、白、黄、绿、蓝、紫,分别代表的是数字-1、-2、-3、-4、-5、-6中的一个数,如图是这个正方体的三种放置方法,若三个正方体下底面所标颜色代表的数字分别是a,b,c,则a+b+c+abc=-85.