题目内容
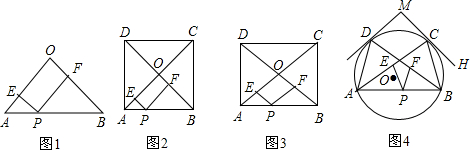
阅读材料:如图1,在△AOB中,∠O=90°,OA=OB,点P在AB边上,PE⊥OA于点E,PF⊥OB于点F,则PE+PF=OA.(此结论不必证明,可直接应用)
(1)【理解与应用】
如图2,正方形ABCD的边长为2,对角线AC,BD相交于点O,点P在AB边上,PE⊥OA于点E,PF⊥OB于点F,则PE+PF的值为 .
(2)【类比与推理】
如图3,矩形ABCD的对角线AC,BD相交于点O,AB=4,AD=3,点P在AB边上,PE∥OB交AC于点E,PF∥OA交BD于点F,求PE+PF的值;
(3)【拓展与延伸】
如图4,⊙O的半径为4,A,B,C,D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF是否为定值?若是,请求出这个定值;若不是,请说明理由.

(1)【理解与应用】
如图2,正方形ABCD的边长为2,对角线AC,BD相交于点O,点P在AB边上,PE⊥OA于点E,PF⊥OB于点F,则PE+PF的值为
(2)【类比与推理】
如图3,矩形ABCD的对角线AC,BD相交于点O,AB=4,AD=3,点P在AB边上,PE∥OB交AC于点E,PF∥OA交BD于点F,求PE+PF的值;
(3)【拓展与延伸】
如图4,⊙O的半径为4,A,B,C,D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF是否为定值?若是,请求出这个定值;若不是,请说明理由.
考点:圆的综合题,等边三角形的判定与性质,矩形的性质,正方形的性质,弦切角定理,相似三角形的判定与性质
专题:压轴题,探究型
分析:(1)易证:OA=OB,∠AOB=90°,直接运用阅读材料中的结论即可解决问题.
(2)易证:OA=OB=OC=0D=
,然后由条件PE∥OB,PF∥AO可证△AEP∽△AOB,△BFP∽△BOA,从而可得
+
=
+
=1,进而求出EP+FP=
.
(3)易证:AD=BC=4.仿照(2)中的解法即可求出PE+PF=4,因而PE+PF是定值.
(2)易证:OA=OB=OC=0D=
| 5 |
| 2 |
| EP |
| OB |
| FP |
| OA |
| AP |
| AB |
| BP |
| AB |
| 5 |
| 2 |
(3)易证:AD=BC=4.仿照(2)中的解法即可求出PE+PF=4,因而PE+PF是定值.
解答:解:(1)如图2 ,
,
∵四边形ABCD是正方形,
∴OA=OB=OC=OD,∠ABC=∠AOB=90°.
∵AB=BC=2,
∴AC=2
.
∴OA=
.
∵OA=OB,∠AOB=90°,PE⊥OA,PF⊥OB,
∴PE+PF=OA=
.

(2)如图3,
∵四边形ABCD是矩形,
∴OA=OB=OC=OD,∠DAB=90°.
∵AB=4,AD=3,
∴BD=5.
∴OA=OB=OC=OD=
.
∵PE∥OB,PF∥AO,
∴△AEP∽△AOB,△BFP∽△BOA.
∴
=
,
=
.
∴
+
=
+
=1.
∴
+
=1.
∴EP+FP=
.
∴PE+PF的值为
.
(3)当∠ADG=∠BCH=30°时,PE+PF是定值.
理由:连接OA、OB、OC、OD,如图4
∵DG与⊙O相切,
∴∠GDA=∠ABD.
∵∠ADG=30°,
∴∠ABD=30°.
∴∠AOD=2∠ABD=60°.
∵OA=OD,
∴△AOD是等边三角形.
∴AD=OA=4.
同理可得:BC=4.
∵PE∥BC,PF∥AD,
∴△AEP∽△ACB,△BFP∽△BDA.
∴
=
,
=
.
∴
+
=
+
=1.
∴
+
=1.
∴PE+PF=4.
∴当∠ADG=∠BCH=30°时,PE+PF=4.
 ,
,∵四边形ABCD是正方形,
∴OA=OB=OC=OD,∠ABC=∠AOB=90°.
∵AB=BC=2,
∴AC=2
| 2 |
∴OA=
| 2 |
∵OA=OB,∠AOB=90°,PE⊥OA,PF⊥OB,
∴PE+PF=OA=
| 2 |

(2)如图3,
∵四边形ABCD是矩形,
∴OA=OB=OC=OD,∠DAB=90°.
∵AB=4,AD=3,
∴BD=5.
∴OA=OB=OC=OD=
| 5 |
| 2 |
∵PE∥OB,PF∥AO,
∴△AEP∽△AOB,△BFP∽△BOA.
∴
| EP |
| OB |
| AP |
| AB |
| FP |
| OA |
| BP |
| AB |
∴
| EP |
| OB |
| FP |
| OA |
| AP |
| AB |
| BP |
| AB |
∴
| EP | ||
|
| FP | ||
|
∴EP+FP=
| 5 |
| 2 |
∴PE+PF的值为
| 5 |
| 2 |
(3)当∠ADG=∠BCH=30°时,PE+PF是定值.
理由:连接OA、OB、OC、OD,如图4

∵DG与⊙O相切,
∴∠GDA=∠ABD.
∵∠ADG=30°,
∴∠ABD=30°.
∴∠AOD=2∠ABD=60°.
∵OA=OD,
∴△AOD是等边三角形.
∴AD=OA=4.
同理可得:BC=4.
∵PE∥BC,PF∥AD,
∴△AEP∽△ACB,△BFP∽△BDA.
∴
| PE |
| BC |
| AP |
| AB |
| PF |
| AD |
| PB |
| AB |
∴
| PE |
| BC |
| PF |
| AD |
| AP |
| AB |
| PB |
| AB |
∴
| PE |
| 4 |
| PF |
| 4 |
∴PE+PF=4.
∴当∠ADG=∠BCH=30°时,PE+PF=4.
点评:本题考查了正方形的性质、矩形的性质、弦切角定理、相似三角形的判定与性质、等边三角形的判定与性质等知识,考查了类比联想的能力,由一定的综合性.要求PE+PF的值,想到将相似所得的比式相加是解决本题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
下列各数中,在-1与-2之间的数是( )
| A、-1 | ||
B、-
| ||
C、-
| ||
| D、-3 |
 如图,在菱形ABCD中,AB=2
如图,在菱形ABCD中,AB=2
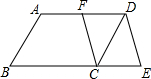 如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE=
如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE= 两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部
两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部 如图,一条直线上有两只蚂蚁,甲蚂蚁在点A处,乙蚂蚁在点B处,假设两只蚂蚁同时出发,爬行方向只能沿直线AB在“向左”或“向右”中随机选择,并且甲蚂蚁爬行的速度比乙蚂蚁快.
如图,一条直线上有两只蚂蚁,甲蚂蚁在点A处,乙蚂蚁在点B处,假设两只蚂蚁同时出发,爬行方向只能沿直线AB在“向左”或“向右”中随机选择,并且甲蚂蚁爬行的速度比乙蚂蚁快.