题目内容
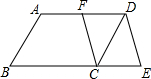 如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE=
如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE=| 1 |
| 2 |
求证:四边形CEDF是平行四边形.
考点:平行四边形的判定与性质
专题:证明题
分析:由“平行四边形的对边平行且相等”的性质推知AD∥BC,且AD=BC;然后根据中点的定义、结合已知条件推知四边形CEDF的对边平行且相等(DF=CE,且DF∥CE),即四边形CEDF是平行四边形.
解答: 证明:如图,在?ABCD中,AD∥BC,且AD=BC.
证明:如图,在?ABCD中,AD∥BC,且AD=BC.
∵F是AD的中点,
∴DF=
.
又∵CE=
BC,
∴DF=CE,且DF∥CE,
∴四边形CEDF是平行四边形.
 证明:如图,在?ABCD中,AD∥BC,且AD=BC.
证明:如图,在?ABCD中,AD∥BC,且AD=BC.∵F是AD的中点,
∴DF=
| 1 |
| 2 |
又∵CE=
| 1 |
| 2 |
∴DF=CE,且DF∥CE,
∴四边形CEDF是平行四边形.
点评:本题考查了平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.

练习册系列答案
相关题目
方程组
的解x、y适合x<0,y>0,则a的取值范围为( )
|
A、a>-
| ||
| B、a>-1 | ||
C、-1<a<-
| ||
| D、a<-1 |
已知a=
+
,b=
-
,则
的值为( )
| 3 |
| 2 |
| 3 |
| 2 |
| a2-ab+b2 |
| A、1 | B、2 | C、3 | D、4 |
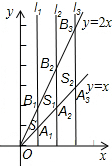 如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3…ln分别交于点A1,A2,A3,…An;函数y=2x的图象与直线l1,l2,l3…ln分别交于点B1,B2,B3…Bn,如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3…四边形An-1AnBnBn-1的面积记作Sn,那么S2014=
如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3…ln分别交于点A1,A2,A3,…An;函数y=2x的图象与直线l1,l2,l3…ln分别交于点B1,B2,B3…Bn,如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3…四边形An-1AnBnBn-1的面积记作Sn,那么S2014=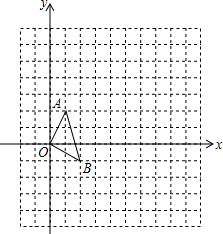 如图,在12×12的正方形网格中,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
如图,在12×12的正方形网格中,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).