Question

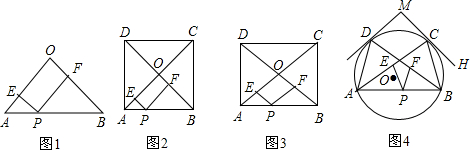
两个城镇A、B与两条公路ME，MF位置如图所示，其中ME是东西方向的公路．现电信部门需在C处修建一座信号发射塔，要求发射塔到两个城镇A、B的距离必须相等，到两条公路ME，MF的距离也必须相等，且在∠FME的内部
（1）那么点C应选在何处？请在图中，用尺规作图找出符合条件的点C．（不写已知、求作、作法，只保留作图痕迹）
（2）设AB的垂直平分线交ME于点N，且MN=2（

3

+1）km，在M处测得点C位于点M的北偏东60°方向，在N处测得点C位于点N的北偏西45°方向，求点C到公路ME的距离．

Answer 1

考点：解直角三角形的应用-方向角问题,作图—应用与设计作图

专题：作图题

分析：（1）到城镇A、B距离相等的点在线段AB的垂直平分线上，到两条公路距离相等的点在两条公路所夹角的角平分线上，分别作出垂直平分线与角平分线，它们的交点即为所求作的点C．
（2）作CD⊥MN于点D，由题意得：∠CMN=30°，∠CND=45°，分别在Rt△CMD中和Rt△CND中，用CD表示出MD和ND的长，从而求得CD的长即可．

解答：解：（1）答图如图：


（2）作CD⊥MN于点D，

由题意得：∠CMN=30°，∠CND=45°，
∵在Rt△CMD中，

CD

MD

=tan∠CMN，
∴MD=

CD

3 3

=

3

CD；
∵在Rt△CND中，

CD

DN

=tan∠CNM，
∴ND=

CD

1

=CD；
∵MN=2（

3

+1）km，
∴MN=MD+DN=CD+

3

CD=2（

3

+1）km，
解得：CD=2km．
故点C到公路ME的距离为2km．

点评：本题考查了解直角三角形的应用及尺规作图，正确的作出图形是解答本题的关键，难度不大．