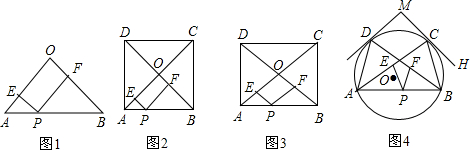
题目内容
如图，在菱形ABCD中，AB=2| 3 |
 |
| EF |
考点：切线的性质,菱形的性质,圆锥的计算
专题：
分析：先连接CG，设CG=R，由勾股定理求得扇形的半径即圆锥的母线长，根据弧长公式l=
，再由2π•r=
，求出底面半径r，则根据勾股定理即可求得圆锥的高．
| nπR |
| 180 |
| nπR |
| 180 |
解答：
解：如图：连接CG，
∵∠C=120°，
∴∠B=60°，
∵AB与相切，
∴CG⊥AB，
在直角△CBG中CG=BC•sin60°=2
×
=3，即圆锥的母线长是3，
设圆锥底面的半径为r，则：2πr=
，
∴r=1．
则圆锥的高是：
=2
．
故答案是：2
．
解：如图：连接CG，∵∠C=120°，
∴∠B=60°，
∵AB与相切，
∴CG⊥AB，
在直角△CBG中CG=BC•sin60°=2
| 3 |
| ||
| 2 |
设圆锥底面的半径为r，则：2πr=
| 120π×3 |
| 180 |
∴r=1．
则圆锥的高是：
| 32-12 |
| 2 |
故答案是：2
| 2 |
点评：本题考查的是圆锥的计算，先利用直角三角形求出扇形的半径，运用弧长公式计算出弧长，然后根据底面圆的周长等于扇形的弧长求出底面圆的半径．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
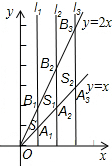如图，直线l1⊥x轴于点（1，0），直线l2⊥x轴于点（2，0），直线l3⊥x轴于点（3，0），…直线ln⊥x轴于点（n，0）．函数y=x的图象与直线l1，l2，l3…ln分别交于点A1，A2，A3，…An；函数y=2x的图象与直线l1，l2，l3…ln分别交于点B1，B2，B3…Bn，如果△OA1B1的面积记作S1，四边形A1A2B2B1的面积记作S2，四边形A2A3B3B2的面积记作S3…四边形An-1AnBnBn-1的面积记作Sn，那么S2014=若A（-1，y1），B（-3，y2）两点都在反比例函数y=
的图象上，则（ ）
| 3 |
| x |
| A、y1＞y2 |
| B、y1＜y2 |
| C、y1≤y2 |
| D、y1≥y2 |
AC，BD是?ABCD的两条对角线，如果添加一个条件，使?ABCD为矩形，那么这个条件可以是（ ）
| A、AB=BC |
| B、AC=BD |
| C、AC⊥BD |
| D、AB⊥BD |
方程组
的解x、y适合x＜0，y＞0，则a的取值范围为（ ）
|
A、a＞-
| ||
| B、a＞-1 | ||
C、-1＜a＜-
| ||
| D、a＜-1 |
