题目内容
8. 如图,每个小正方形的边长均为1.
如图,每个小正方形的边长均为1.(1)图中阴影部分的面积是多少?
(2)图中阴影部分四边形边长是多少?估计边长的值在哪两个整数之间.
分析 (1)由大正方形的面积减去4个直角三角形的面积即可;
(2)由勾股定理即可得出正方形的边长,通过估算无理数,即可得出结果.
解答 解:(1)图中阴影部分的面积=5×5-4×$\frac{1}{2}$×1×4=17;
(2)图中四边形的边长=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$;
∵$\sqrt{16}$<$\sqrt{17}$<$\sqrt{25}$,
∴4<$\sqrt{17}$<5,
即阴影部分四边形的边长的值在4与5之间.
点评 本题考查了勾股定理、正方形的性质以及估算无理数的大小;熟练掌握正方形的性质,运用勾股定理求出边长是解决问题的关键.

练习册系列答案
相关题目
18. 如图,一种花边是由如图的弓形组成的,弦AB=8,弓形的高CD为2,则弧ACB的半径为( )
如图,一种花边是由如图的弓形组成的,弦AB=8,弓形的高CD为2,则弧ACB的半径为( )
 如图,一种花边是由如图的弓形组成的,弦AB=8,弓形的高CD为2,则弧ACB的半径为( )
如图,一种花边是由如图的弓形组成的,弦AB=8,弓形的高CD为2,则弧ACB的半径为( )| A. | 8 | B. | 2 | C. | 5 | D. | 4 |
16.△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定△ABC为直角三角形的是( )
| A. | ∠A:∠B:∠C=l:2:3 | B. | 三边长为a,b,c的值为1,2,$\sqrt{3}$ | ||
| C. | 三边长为a,b,c的值为$\sqrt{11}$,2,4 | D. | a2=(c+b)(c-b) |
5.九年级某数学兴趣小组通过市场调查,得到某种运动服每月的销量与售价的相关信息如表:
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:销售该运动服每件的利润是x-60元(直接写出结果);
(2)猜想月销量y与售价x之间是什么函数关系?并求出函数关系式;
(3)设销售该运动服的月利润为w元,那么售价x为多少时,当月的利润最大,最大利润是多少?
| 售价(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量(件) | 200 | 180 | 160 | 140 | … |
(1)请用含x的式子表示:销售该运动服每件的利润是x-60元(直接写出结果);
(2)猜想月销量y与售价x之间是什么函数关系?并求出函数关系式;
(3)设销售该运动服的月利润为w元,那么售价x为多少时,当月的利润最大,最大利润是多少?
 如图,点A、B、C在⊙O上,∠C=115°,则∠AOB=130°.
如图,点A、B、C在⊙O上,∠C=115°,则∠AOB=130°.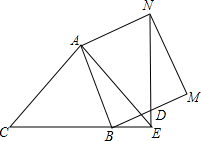 如图,等腰直角△ACE,AC=AE=4$\sqrt{2}$,∠CAE=90°,点B是CE上一点,以AB为边向外作正方形ABMN,连接NE交BD于点D.
如图,等腰直角△ACE,AC=AE=4$\sqrt{2}$,∠CAE=90°,点B是CE上一点,以AB为边向外作正方形ABMN,连接NE交BD于点D.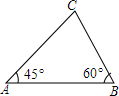 如图,△ABC中,∠A=45°,∠B=60°,AB=100cm,求△ABC的面积.
如图,△ABC中,∠A=45°,∠B=60°,AB=100cm,求△ABC的面积. 如图,一次函数y=kx+b与y=mx+n的图象交于点P(2,-1),则由函数图象得不等式kx+b≥mx+n的解集为x≥2.
如图,一次函数y=kx+b与y=mx+n的图象交于点P(2,-1),则由函数图象得不等式kx+b≥mx+n的解集为x≥2.