题目内容
13.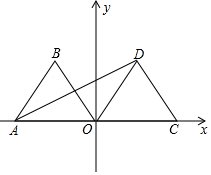 如图,在平面直角坐标系中,点A(-2,0),等边△AOB经过平移或轴对称或旋转都可以得到△OCD.
如图,在平面直角坐标系中,点A(-2,0),等边△AOB经过平移或轴对称或旋转都可以得到△OCD.(1)填空:
①△AOB沿x轴向右平移得到△OCD,则平移的距离是2个单位长度;
②△AOB与△OCD关于某直线对称,则对称轴是y轴;
③△AOB绕原点O顺时针旋转得到△OCD,则旋转角度可以是120度;
(2)连接AD,请探索AD与CD的位置关系.
分析 (1)平移的距离为对应点连线的长度,对称轴为对应点连线的垂直平分线,旋转角为对应点与旋转中心连线的夹角的大小,据此判断即可;
(2)连接AD后可得底角为30°的等腰三角形AOD,进而可得∠ADC为直角,再根据勾股定理求得直角边AD的长.
解答 解:(1)△AOB沿x轴向右平移得到△OCD,根据AO=2可知,平移的距离是2个单位长度;
△AOB与△COD关于直线对称,根据线段AC被y轴垂直平分可知,对称轴是y轴;
△AOB绕原点O顺时针旋转得到△DOC,根据∠BOC=180°-∠AOB=120°可知,旋转角度可以是120°;
故答案为:2;y轴;120
(2)由AO=DO,∠COD=60°可得,∠OAD=∠ODA=30°,
∴∠ADC=30°+60°=90°,
∴AD⊥CD.
点评 此题是几何变换综合题,主要考查了图形的基本变换与坐标以及等边三角形的性质,解题时需要注意:平移的距离等于对应点连线的长度,对称轴为对应点连线的垂直平分线,旋转角为对应点与旋转中心连线的夹角的大小.

练习册系列答案
相关题目
8.为了保护生态平衡,绿化环境,国家大力鼓励“退耕还林、还草”,其补偿政策如表(一):某农户承包了一片山坡地种树种草,所得到的国家的补偿如表(二).
表(一)种树、种草每亩每年补粮补钱情况表
表(二)该农户收到乡政府下发的当种树种草亩数及年补偿通知单
(1)该农户当年种树、种草各多少亩?
(2)若今年该农户又扩展40亩山坡地种树种草,要想年终政府补钱不少于12000元,至少需要安排多少亩山坡地种树?
表(一)种树、种草每亩每年补粮补钱情况表
| 种树 | 种草 | |
| 补粮 | 150千克 | 100千克 |
| 补钱 | 200元 | 150元 |
| 种树、种草 | 补粮 | 补钱 |
| 30亩 | 4000千克 | 5500元 |
(2)若今年该农户又扩展40亩山坡地种树种草,要想年终政府补钱不少于12000元,至少需要安排多少亩山坡地种树?
 如图,在四边形ABCD中,AD∥BC,对角线AC⊥BD,若AD=6,BC=14,则四边形ABCD面积的最大值是100.
如图,在四边形ABCD中,AD∥BC,对角线AC⊥BD,若AD=6,BC=14,则四边形ABCD面积的最大值是100.
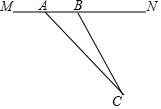 目前,我市正在积极创建文明城市,交通部门一再提醒司机:为了安全,请勿超速,并再进一步完善各类监测系统,如图,在某公路直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73)
目前,我市正在积极创建文明城市,交通部门一再提醒司机:为了安全,请勿超速,并再进一步完善各类监测系统,如图,在某公路直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73) 如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.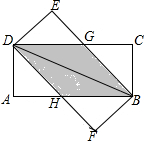 将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG,
将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG,