题目内容
2.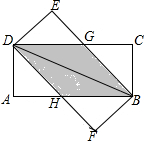 将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG,
将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG,(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若AB=8,AD=4,求四边形DHBG的面积.
分析 (1)由四边形ABCD、FBED是完全相同的矩形,可得出△DAB≌△DEB(SAS),进而可得出∠ABD=∠EBD,根据矩形的性质可得AB∥CD、DF∥BE,即四边形DHBG是平行四边形,再根据平行线的性质结合∠ABD=∠EBD,即可得出∠HDB=∠HBD,由等角对等边可得出DH=BH,由此即可证出?DHBG是菱形;
(2)设DH=BH=x,则AH=8-x,在Rt△ADH中,利用勾股定理即可得出关于x的一元一次方程,解之即可得出x的值,再根据菱形的面积公式即可求出菱形DHBG的面积.
解答 解:(1)四边形DHBG是菱形.理由如下:
∵四边形ABCD、FBED是完全相同的矩形,
∴∠A=∠E=90°,AD=ED,AB=EB.
在△DAB和△DEB中,$\left\{\begin{array}{l}{AD=ED}\\{∠A=∠E}\\{AB=EB}\end{array}\right.$,
∴△DAB≌△DEB(SAS),
∴∠ABD=∠EBD.
∵AB∥CD,DF∥BE,
∴四边形DHBG是平行四边形,∠HDB=∠EBD,
∴∠HDB=∠HBD,
∴DH=BH,
∴?DHBG是菱形.
(2)由(1),设DH=BH=x,则AH=8-x,
在Rt△ADH中,AD2+AH2=DH2,即42+(8-x)2=x2,
解得:x=5,即BH=5,
∴菱形DHBG的面积为HB•AD=5×4=20.
点评 本题考查了菱形的判定与性质、矩形的性质、全等三角形的判定与性质以及勾股定理,解题的关键是:(1)利用等角对等边找出DH=BH;(2)利用勾股定理求出菱形的边长.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
14.如果10b=n,那么b为n的劳格数,记为b=d(n),由定义可知:10b=n与b=d(n)所表示的b、n两个量之间的同一关系.例如:101=10,d(10)=1
(1)根据劳格数的定义,填空:d(102)=2,
(2)劳格数有如下运算性质:若m、n为正数,则d(mn)=d(m)+d(n),d($\frac{m}{n}$ )=d(m)-d(n).
根据运算性质,填空:$\frac{d({a}^{3})}{d(a)}$=3(a为正数),若d(2)=0.3010,则d(16)=1.204,d(5)=0.6990,
(3)如表中与数x对应的劳格数d(x)有且只有两个是错误的
请找出错误的劳格数,并表格中直接改正.
(1)根据劳格数的定义,填空:d(102)=2,
(2)劳格数有如下运算性质:若m、n为正数,则d(mn)=d(m)+d(n),d($\frac{m}{n}$ )=d(m)-d(n).
根据运算性质,填空:$\frac{d({a}^{3})}{d(a)}$=3(a为正数),若d(2)=0.3010,则d(16)=1.204,d(5)=0.6990,
(3)如表中与数x对应的劳格数d(x)有且只有两个是错误的
| x | 1.5 | 3 | 5 | 6 | 8 | 9 | 18 | 27 |
| d(x) | 3a-b+c | 2a+b | a-c | 1+a+b+c | 3-3a+3c | 4a+2b | 3-b-2c | 6a+3b |
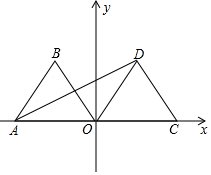 如图,在平面直角坐标系中,点A(-2,0),等边△AOB经过平移或轴对称或旋转都可以得到△OCD.
如图,在平面直角坐标系中,点A(-2,0),等边△AOB经过平移或轴对称或旋转都可以得到△OCD.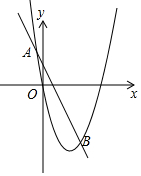 如图,在平面直角坐标系中,点A(-1,n)与点B(2,n),在抛物线y=x2-3x上,
如图,在平面直角坐标系中,点A(-1,n)与点B(2,n),在抛物线y=x2-3x上,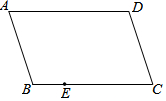 如图,四边形ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.
如图,四边形ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.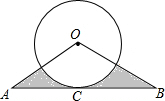 如图,在△ABC中,OA=OB=6,∠O=120°,以点O为圆心的⊙O和底边AB相切于点C,则阴影部分的面积为9$\sqrt{3}$-3π..
如图,在△ABC中,OA=OB=6,∠O=120°,以点O为圆心的⊙O和底边AB相切于点C,则阴影部分的面积为9$\sqrt{3}$-3π..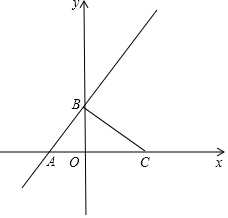 如图,在平面直角坐标系xOy中,点C的坐标为(4,0),一次函数y=$\frac{4}{3}$x+3的图象分别交x轴,y轴于点A,点B.
如图,在平面直角坐标系xOy中,点C的坐标为(4,0),一次函数y=$\frac{4}{3}$x+3的图象分别交x轴,y轴于点A,点B.