题目内容
5. 如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(1)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(2)当t为何值时,△DEF为直角三角形?请说明理由.
分析 (1)能.首先证明四边形AEFD为平行四边形,当AE=AD时,四边形AEFD为菱形,即60-4t=2t,解方程即可解决问题;
(2)分三种情形讨论即可.
解答 (1)证明:能.
理由如下:在△DFC中,∠DFC=90°,∠C=30°,DC=4t,
∴DF=2t,
又∵AE=2t,
∴AE=DF,
∵AB⊥BC,DF⊥BC,
∴AE∥DF,
又∵AE=DF,
∴四边形AEFD为平行四边形,
当AE=AD时,四边形AEFD为菱形,
即60-4t=2t,解得t=10.
∴当t=10秒时,四边形AEFD为菱形.
(2)①当∠DEF=90°时,由(1)知四边形AEFD为平行四边形,
∴EF∥AD,
∴∠ADE=∠DEF=90°,
∵∠A=60°,
∴∠AED=30°,
∴AD=$\frac{1}{2}$AE=t,
又AD=60-4t,即60-4t=t,解得t=12;
②当∠EDF=90°时,四边形EBFD为矩形,在Rt△AED中∠A=60°,则∠ADE=30°,
∴AD=2AE,即60-4t=4t,解得t=$\frac{15}{2}$.
③若∠EFD=90°,则E与B重合,D与A重合,此种情况不存在.
综上所述,当t=$\frac{15}{2}$或12秒时,△DEF为直角三角形.
点评 本题考查平行四边形的判定和性质、菱形的判定、直角三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会构建方程解决问题,属于中考常考题型.

练习册系列答案
相关题目
16. 如图中的两个三角形全等,则∠1=( )
如图中的两个三角形全等,则∠1=( )
 如图中的两个三角形全等,则∠1=( )
如图中的两个三角形全等,则∠1=( )| A. | 45° | B. | 58° | C. | 76° | D. | 77° |
14.如果10b=n,那么b为n的劳格数,记为b=d(n),由定义可知:10b=n与b=d(n)所表示的b、n两个量之间的同一关系.例如:101=10,d(10)=1
(1)根据劳格数的定义,填空:d(102)=2,
(2)劳格数有如下运算性质:若m、n为正数,则d(mn)=d(m)+d(n),d($\frac{m}{n}$ )=d(m)-d(n).
根据运算性质,填空:$\frac{d({a}^{3})}{d(a)}$=3(a为正数),若d(2)=0.3010,则d(16)=1.204,d(5)=0.6990,
(3)如表中与数x对应的劳格数d(x)有且只有两个是错误的
请找出错误的劳格数,并表格中直接改正.
(1)根据劳格数的定义,填空:d(102)=2,
(2)劳格数有如下运算性质:若m、n为正数,则d(mn)=d(m)+d(n),d($\frac{m}{n}$ )=d(m)-d(n).
根据运算性质,填空:$\frac{d({a}^{3})}{d(a)}$=3(a为正数),若d(2)=0.3010,则d(16)=1.204,d(5)=0.6990,
(3)如表中与数x对应的劳格数d(x)有且只有两个是错误的
| x | 1.5 | 3 | 5 | 6 | 8 | 9 | 18 | 27 |
| d(x) | 3a-b+c | 2a+b | a-c | 1+a+b+c | 3-3a+3c | 4a+2b | 3-b-2c | 6a+3b |
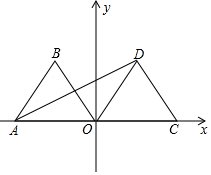 如图,在平面直角坐标系中,点A(-2,0),等边△AOB经过平移或轴对称或旋转都可以得到△OCD.
如图,在平面直角坐标系中,点A(-2,0),等边△AOB经过平移或轴对称或旋转都可以得到△OCD.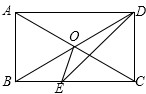 如图,矩形ABCD中,AC、BD交于点O,∠AOB=60°,DE平分∠ADC交BC于点E,连接OE,则∠COE=75°.
如图,矩形ABCD中,AC、BD交于点O,∠AOB=60°,DE平分∠ADC交BC于点E,连接OE,则∠COE=75°.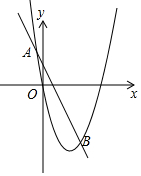 如图,在平面直角坐标系中,点A(-1,n)与点B(2,n),在抛物线y=x2-3x上,
如图,在平面直角坐标系中,点A(-1,n)与点B(2,n),在抛物线y=x2-3x上,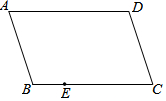 如图,四边形ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.
如图,四边形ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.