题目内容
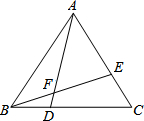 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.求证:BD2=AD•DF.
如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.求证:BD2=AD•DF.考点:相似三角形的判定与性质,等边三角形的性质
专题:证明题
分析:利用等边三角形的性质可证明△ABD≌△BCE,可得∠FBD=∠BAD,可证明△BDF∽△ADB,可得
=
,可得出结论.
| BD |
| AD |
| DF |
| BD |
解答:证明:∵△ABC为等边三角形,
∴AB=BC,∠ABC=∠C,
在△ABD和△BCE中,
,
∴△ABD≌△BCE(SAS),
∴∠FBD=∠BAD,且∠BDF=∠ADB,
∴△BDF∽△ADB,
∴
=
,
∴BD2=AD•DF.
∴AB=BC,∠ABC=∠C,
在△ABD和△BCE中,
|
∴△ABD≌△BCE(SAS),
∴∠FBD=∠BAD,且∠BDF=∠ADB,
∴△BDF∽△ADB,
∴
| BD |
| AD |
| DF |
| BD |
∴BD2=AD•DF.
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的判定方法是解题关键,注意化线段乘积为比例再证明相似是解决这类问题的基本思路0

练习册系列答案
相关题目
当a<0时,抛物线y=x2+2ax+a2+1的顶点在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
抛物线y=(x-2)2-2的顶点坐标是( )
| A、(-2,2) |
| B、(2,-2) |
| C、(2,2) |
| D、(-2,-2) |
 如图所示,已知一个圆的外切正方形的边长为4cm,求这个圆的内接正三角形的边心距?边长?
如图所示,已知一个圆的外切正方形的边长为4cm,求这个圆的内接正三角形的边心距?边长?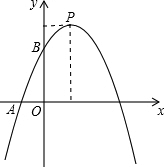 抛物线y=ax2-2ax与x轴正半轴交于B、C为顶点,且点C的纵坐标为2.
抛物线y=ax2-2ax与x轴正半轴交于B、C为顶点,且点C的纵坐标为2. 如图,若四边形ABCD是半径为1厘米和⊙O的内接正方形,则图中四个弓形(即四个阴影部分)的面积之和为
如图,若四边形ABCD是半径为1厘米和⊙O的内接正方形,则图中四个弓形(即四个阴影部分)的面积之和为 如图,四边形ABCD中,∠ADB=∠ABC=105°,∠DBC=75°,AB=DC=15,则S△BCD为
如图,四边形ABCD中,∠ADB=∠ABC=105°,∠DBC=75°,AB=DC=15,则S△BCD为