题目内容
 如图所示,已知一个圆的外切正方形的边长为4cm,求这个圆的内接正三角形的边心距?边长?
如图所示,已知一个圆的外切正方形的边长为4cm,求这个圆的内接正三角形的边心距?边长?考点:正多边形和圆
专题:
分析:连接OG,过点O作OE⊥GF于点E,根据圆的外切正方形的边长为4cm可知OG=2cm,根据直角三角形的性质可得出OE及GE的长,进而得出GF的长.
解答: 解:连接OG,过点O作OE⊥GF于点E,
解:连接OG,过点O作OE⊥GF于点E,
∵圆的外切正方形的边长为4cm,
∴OG=2cm.
∵△FHF是正三角形,
∴∠OGE=30°,
∴OE=
OG=1m,GE=OG•cos30°=1×
=
,
∴GF=2GE=
.
 解:连接OG,过点O作OE⊥GF于点E,
解:连接OG,过点O作OE⊥GF于点E,∵圆的外切正方形的边长为4cm,
∴OG=2cm.
∵△FHF是正三角形,
∴∠OGE=30°,
∴OE=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴GF=2GE=
| 3 |
点评:本题考查的是正多边形和圆,熟知等边三角形及正方形的性质是解答此题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
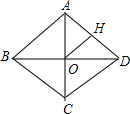 如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为32,则OH的长等于( )
如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为32,则OH的长等于( )| A、4 | B、8 | C、16 | D、18 |
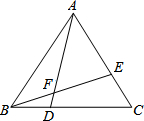 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.求证:BD2=AD•DF.
如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.求证:BD2=AD•DF. 如图,⊙O的半径为5,P是CB延长线上一点,PO=13,PA切⊙O于A点,则PA=
如图,⊙O的半径为5,P是CB延长线上一点,PO=13,PA切⊙O于A点,则PA= 如图,若图中所有的三角形都是直角三角形,且∠A=α,AE=1,求AB的长.
如图,若图中所有的三角形都是直角三角形,且∠A=α,AE=1,求AB的长.