题目内容
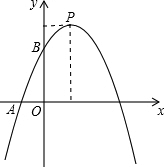 抛物线y=ax2-2ax与x轴正半轴交于B、C为顶点,且点C的纵坐标为2.
抛物线y=ax2-2ax与x轴正半轴交于B、C为顶点,且点C的纵坐标为2.(1)求此抛物线的解析式;
(2)点P为抛物线上一点,且△OPC是以OC为直角边的直角三角形,求点P的坐标.
考点:抛物线与x轴的交点,待定系数法求二次函数解析式
专题:计算题
分析:(1)先把y=ax2-2ax配成顶点式,然后根据顶点的纵坐标为2求出a的值,即可得到抛物线解析式;
(2)根据抛物线上点的坐标特征设P点坐标为(x,-2x2+4x),再利用两点间的距离公式得到OP2=x2+(-2x2+4x)2,PC2=(x-1)2+(-2x2+4x-2)2,
再分类讨论:当∠PCO=90°时,根据勾股定理得OC2+PC2=OP2;当∠POC=90°时,根据勾股定理OC2+PO2=CP2,然后分别得到x的一元二次方程,解方程求出x即可得到满足条件的P点坐标.
(2)根据抛物线上点的坐标特征设P点坐标为(x,-2x2+4x),再利用两点间的距离公式得到OP2=x2+(-2x2+4x)2,PC2=(x-1)2+(-2x2+4x-2)2,
再分类讨论:当∠PCO=90°时,根据勾股定理得OC2+PC2=OP2;当∠POC=90°时,根据勾股定理OC2+PO2=CP2,然后分别得到x的一元二次方程,解方程求出x即可得到满足条件的P点坐标.
解答: 解:(1)∵y=a(x-1)2-a,
解:(1)∵y=a(x-1)2-a,
∴顶点C的坐标为(1,-a),
而C的纵坐标为2,
∴-a=2,解得a=-2,
∴抛物线解析式为y=-2x2+4x;
(2)设P点坐标为(x,-2x2+4x),
而C(1,2),
则OC2=12+22=5,OP2=x2+(-2x2+4x)2,PC2=(x-1)2+(-2x2+4x-2)2,
当∠PCO=90°时,OC2+PC2=OP2,即5+(x-1)2+(-2x2+4x-2)2=x2+(-2x2+4x)2,
整理得4x2-9x+5=0,解得x1=1(舍去),x2=
,
此时P点坐标为(
,
);
当∠POC=90°时,OC2+PO2=CP2,即5+x2+(-2x2+4x)2=(x-1)2+(-2x2+4x-2)2,
整理得4x2-9x=0,解得x1=0(舍去),x2=
,
此时P点坐标为(
,-
),
综上所述,满足条件的P点坐标为(
,
)或(
,-
).
 解:(1)∵y=a(x-1)2-a,
解:(1)∵y=a(x-1)2-a,∴顶点C的坐标为(1,-a),
而C的纵坐标为2,
∴-a=2,解得a=-2,
∴抛物线解析式为y=-2x2+4x;
(2)设P点坐标为(x,-2x2+4x),
而C(1,2),
则OC2=12+22=5,OP2=x2+(-2x2+4x)2,PC2=(x-1)2+(-2x2+4x-2)2,
当∠PCO=90°时,OC2+PC2=OP2,即5+(x-1)2+(-2x2+4x-2)2=x2+(-2x2+4x)2,
整理得4x2-9x+5=0,解得x1=1(舍去),x2=
| 5 |
| 4 |
此时P点坐标为(
| 5 |
| 4 |
| 15 |
| 8 |
当∠POC=90°时,OC2+PO2=CP2,即5+x2+(-2x2+4x)2=(x-1)2+(-2x2+4x-2)2,
整理得4x2-9x=0,解得x1=0(舍去),x2=
| 9 |
| 4 |
此时P点坐标为(
| 9 |
| 4 |
| 9 |
| 8 |
综上所述,满足条件的P点坐标为(
| 5 |
| 4 |
| 15 |
| 8 |
| 9 |
| 4 |
| 9 |
| 8 |
点评:本题考查了抛物线与x轴的交点:二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系,△=b2-4ac决定抛物线与x轴的交点个数.也考查了两点间的距离公式和勾股定理.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
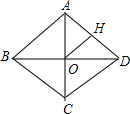 如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为32,则OH的长等于( )
如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为32,则OH的长等于( )| A、4 | B、8 | C、16 | D、18 |
 如图,小明和小华玩跷跷板游戏,若跷跷板中点O(支点)到地面的距离OD=50cm,当小华从水平位置下降到地面时,小明这时离地面的高度为
如图,小明和小华玩跷跷板游戏,若跷跷板中点O(支点)到地面的距离OD=50cm,当小华从水平位置下降到地面时,小明这时离地面的高度为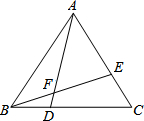 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.求证:BD2=AD•DF.
如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.求证:BD2=AD•DF. 如图,⊙O的半径为5,P是CB延长线上一点,PO=13,PA切⊙O于A点,则PA=
如图,⊙O的半径为5,P是CB延长线上一点,PO=13,PA切⊙O于A点,则PA=