题目内容
 如图,若四边形ABCD是半径为1厘米和⊙O的内接正方形,则图中四个弓形(即四个阴影部分)的面积之和为
如图,若四边形ABCD是半径为1厘米和⊙O的内接正方形,则图中四个弓形(即四个阴影部分)的面积之和为考点:扇形面积的计算
专题:
分析:如图,作辅助线,首先求出△AOD的面积、扇形AOD的面积,进而求出弓形AD的面积问题即可解决.
解答: 解:如图,连接OA、OD;
解:如图,连接OA、OD;
过点O作OE⊥AD于点E,
∵四边形ABCD为正方形,
∴∠AOD=90°,∠OAE=45°,
∴∠AOE=∠OAE=45°,而OA=1
∴OE=AE=
,AD=
,
∵S扇形AOD=
=
,
S△AOD=
×
×
=
,
∴S弓形AD=
-
;
同理可求其它三个弓形的面积也为
-
,
∴图中四个弓形(即四个阴影部分)的面积之和为4(
-
)=π-2(cm2),
故答案为π-2
 解:如图,连接OA、OD;
解:如图,连接OA、OD;过点O作OE⊥AD于点E,
∵四边形ABCD为正方形,
∴∠AOD=90°,∠OAE=45°,
∴∠AOE=∠OAE=45°,而OA=1
∴OE=AE=
| ||
| 2 |
| 2 |
∵S扇形AOD=
| 90π×12 |
| 360 |
| π |
| 4 |
S△AOD=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∴S弓形AD=
| π |
| 4 |
| 1 |
| 2 |
同理可求其它三个弓形的面积也为
| π |
| 4 |
| 1 |
| 2 |
∴图中四个弓形(即四个阴影部分)的面积之和为4(
| π |
| 4 |
| 1 |
| 2 |
故答案为π-2
点评:该题以圆为载体,以扇形面积的计算为考查的核心构造而成;解题的关键是,作辅助线,将弓形面积的计算问题转化为扇形面积的计算问题.

练习册系列答案
相关题目
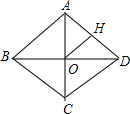 如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为32,则OH的长等于( )
如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为32,则OH的长等于( )| A、4 | B、8 | C、16 | D、18 |
 如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是( )
如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是( )| A、AB=AC |
| B、BE=CD |
| C、角B=角C |
| D、角ADC=角AEB |
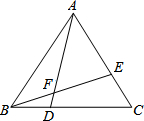 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.求证:BD2=AD•DF.
如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.求证:BD2=AD•DF.