题目内容
设计三个直径相等的轧辊,使它们能够把直径为4mm的滚轴轧紧.求轧辊的半径r(精确到到0.01mm).(注:三个圆心连起来是正三角形,滚轴在三个轧辊的中间.)
考点:相切两圆的性质
专题:应用题
分析:设轧辊断面的半径为r,中心分别为O1、O2、O3滚轴断面的中心为O,连接OA,根据勾股定理列出方程,再进行求解即可.
解答: 解:设轧辊断面的半径为r,中心分别为O1、O2、O3滚轴断面的中心为O,连接OA,
解:设轧辊断面的半径为r,中心分别为O1、O2、O3滚轴断面的中心为O,连接OA,
则∠OO1A=30°,OA=
OO1=
(2+r),
根据勾股定理得:(2+r)2=[
(2+r)]2=r2,
整理得:r2-12r-12=0,
解得;r1=6-4
(舍去),r2=6+4
≈12.93(mm).
则轧辊的半径12.93mm.
 解:设轧辊断面的半径为r,中心分别为O1、O2、O3滚轴断面的中心为O,连接OA,
解:设轧辊断面的半径为r,中心分别为O1、O2、O3滚轴断面的中心为O,连接OA,则∠OO1A=30°,OA=
| 1 |
| 2 |
| 1 |
| 2 |
根据勾股定理得:(2+r)2=[
| 1 |
| 2 |
整理得:r2-12r-12=0,
解得;r1=6-4
| 3 |
| 3 |
则轧辊的半径12.93mm.
点评:本题考查了相切两圆的性质,用到的知识点是相切两圆的连心线长等于两圆半径,圆的半径垂直于过切点的半径,勾股定理等,关键是根据题意画出图形构造直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ACD中,∠C=90°,∠D=15°,点B是线段AD的垂直平分线与CD的交点,若AC=4,则BD的长为( )
如图,在△ACD中,∠C=90°,∠D=15°,点B是线段AD的垂直平分线与CD的交点,若AC=4,则BD的长为( ) 如图,在△ABC中,AB=5,D、E分别是边AC和AB上的点,且∠ADE=∠B,DE=2,那么AD•BC=
如图,在△ABC中,AB=5,D、E分别是边AC和AB上的点,且∠ADE=∠B,DE=2,那么AD•BC=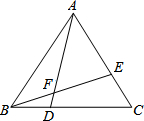 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.求证:BD2=AD•DF.
如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.求证:BD2=AD•DF. 如图,在Rt△ABC中,∠C=90°,AD是中线,若AC=3cm,BC=4cm,则△ABD的面积是
如图,在Rt△ABC中,∠C=90°,AD是中线,若AC=3cm,BC=4cm,则△ABD的面积是 两龙”高速公路是目前我省高速公路隧道和桥梁最多的路段,如图,是一个单心圆曲隧道的截面.若路面AB宽为10米,净高CD为7米,求圆的半径.
两龙”高速公路是目前我省高速公路隧道和桥梁最多的路段,如图,是一个单心圆曲隧道的截面.若路面AB宽为10米,净高CD为7米,求圆的半径.