题目内容
当a＜0时，抛物线y=x2+2ax+a2+1的顶点在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点：二次函数的性质
专题：
分析：把二次函数的解析式化为顶点式，得出顶点坐标，再结合a＜0进行判断即可．
解答：解：
∵y=x2+2ax+a2+1=（x+a）2+1，
∴抛物线的顶点坐标为（-a，1），
∵a＜0，
∴-a＞0，
∴（-a，1）在第一象限，
故选A．
∵y=x2+2ax+a2+1=（x+a）2+1，
∴抛物线的顶点坐标为（-a，1），
∵a＜0，
∴-a＞0，
∴（-a，1）在第一象限，
故选A．
点评：本题主要考查二次函数的顶点坐标，掌握二次函数的顶点式y=a（x-h）2+k是解题的关键．
练习册系列答案
相关题目
在有理数-
，1.2，-2，0，-（-2）中，负数的个数有（ ）
| 3 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
如图，小明和小华玩跷跷板游戏，若跷跷板中点O（支点）到地面的距离OD=50cm，当小华从水平位置下降到地面时，小明这时离地面的高度为
如图，在△ABC中，AB=5，D、E分别是边AC和AB上的点，且∠ADE=∠B，DE=2，那么AD•BC=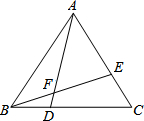
如图，△ABC是等边三角形，点D、E分别在BC、AC上，且BD=CE，AD与BE相交于点F．求证：BD2=AD•DF．