题目内容
12．
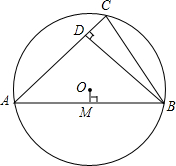如图，已知⊙O的半径为1，锐角△ABC内接于⊙O，BD⊥AC于点D，OM⊥AB于点M，OM的长为0.3，求sin∠CBD的值．
分析 作直径AE，连接BE．得直角三角形ABE．根据圆周角定理可证∠CBD=∠MAO，运用三角函数定义求解．
解答 解：连接AO并延长交⊙O于点E，连接BE．如图所示：
则∠C=∠E，
yw5AE为直径，BD⊥AC，
∴∠BDC=∠ABE=90°，
即△ABE和△BCD都是直角三角形，
∴∠CBD=∠EAB．
又△OAM是直角三角形，AO=1，
∴sin∠CBD=sin∠EAB=$\frac{OM}{OA}$=0.3．
点评 本题考查了圆周角定理和三角函数定义．通过作辅助线运用圆周角定理证出∠CBD=∠EAB是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知一次函数y=kx+b的图象与x轴交于点A（5，0），与函数y=2x的图象交于点M，点M的横坐标为2，求点M的坐标及函数y=kx+b的表达式．
20．已知正△ABC内接于圆O，四边形DEFG为半圆O的内接正方形（D，E在直径上，F，G在半圆上的正方形），S△ABC=a，S四边形DEFG=b，则$\frac{a}{b}$的值等于（ ）
| A． | 2 | B． | $\frac{\sqrt{6}}{2}$ | C． | $\frac{3\sqrt{3}}{5}$ | D． | $\frac{15\sqrt{3}}{16}$ |
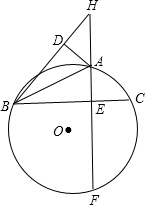如图，△ABC内接于⊙O，AE和BD是它的两条高，相交于点H，直线AH交⊙O于点F，求证：EH=EF．
