题目内容
20.已知正△ABC内接于圆O,四边形DEFG为半圆O的内接正方形(D,E在直径上,F,G在半圆上的正方形),S△ABC=a,S四边形DEFG=b,则$\frac{a}{b}$的值等于( )| A. | 2 | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{3\sqrt{3}}{5}$ | D. | $\frac{15\sqrt{3}}{16}$ |
分析 设圆O的半径为R,由正三角形的性质得出S△ABC=a=$\frac{3\sqrt{3}}{4}$RR2,连接OF,设正方形DEFG的边长为2x,则OE=x,由勾股定理和正方形的性质得出x2=$\frac{{R}^{2}}{5}$,得出正方形DEFG的面积b=$\frac{4}{5}{R}^{2}$,即可得出结果.
解答 解:如图所示: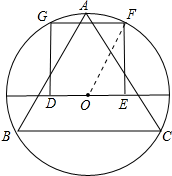 连接OF,
连接OF,
设圆O的半径为R,
∵△ABC是正三角形,
∴S△ABC=a=$\frac{3\sqrt{3}}{4}$R2,
设正方形DEFG的边长为2x,则OE=x,
∴OF2=OE2+EF2=x2+(2x)2=5x2,
即R2=5x2,
∴x2=$\frac{{R}^{2}}{5}$,
∴正方形DEFG的面积=(2x)2=4x2=$\frac{4}{5}$R2,
即b=$\frac{4}{5}$R2,
∴$\frac{a}{b}$=$\frac{\frac{3\sqrt{3}}{4}{R}^{3}}{\frac{4}{5}{R}^{2}}$=$\frac{15\sqrt{3}}{16}$.
故选:D.
点评 本题考查了正三角形的性质、正方形的性质、正多边形和圆的关系、勾股定理等知识;本题综合性强,有一定难度,把正三角形和正方形的面积用半径R表示出来是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
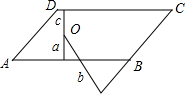 如图,在平行四边形ABCD中,AB=2AD,点O为平行四边形内一点,它到直线AB,BC,CD距离分别为a,b,c,且它到AD和CD的距离相等,则2a-b+c=0.
如图,在平行四边形ABCD中,AB=2AD,点O为平行四边形内一点,它到直线AB,BC,CD距离分别为a,b,c,且它到AD和CD的距离相等,则2a-b+c=0.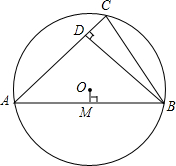 如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,OM的长为0.3,求sin∠CBD的值.
如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,OM的长为0.3,求sin∠CBD的值.