题目内容
2.观察下面的点阵图和相应的等式,探究其中的规律:(1)认真观察,并在④后面的横线上写出相应的等式.

①1=1;②1+2=$\frac{{({1+2})×2}}{2}$;③1+2+3=$\frac{{({1+3})×3}}{2}$;④1+2+3+4=$\frac{(1+4)×4}{2}$
(2)结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.

(3)通过猜想,写出(2)中与第n个点阵相对应的等式$\frac{n(n-1)}{2}$+$\frac{n(n+1)}{2}$=n2.
①1=12;②1+3=22;③3+6=32; ④6+10=42; ⑤10+15=52;…
分析 通过对一些特殊式子进行整理、变形、观察、比较,归纳出一般规律.
解答 解:(1)根据题中所给出的规律可知:1+2+3+4=$\frac{(1+4)×4}{2}$;
(2)由图示可知点的总数是5×5=25,所以10+15=52.
(3)由(1)(2)可知$\frac{n(n-1)}{2}$+$\frac{n(n+1)}{2}$=n2.
故答案为:(1)1+2+3+4=$\frac{(1+4)×4}{2}$;(2)10+15=52;(3)$\frac{n(n-1)}{2}$+$\frac{n(n+1)}{2}$=n2.
点评 主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目中的难点.

练习册系列答案
相关题目
11.已知点(-3,y1),(2,y2)都在直线y=-3x+2b上,则y1、y2的大小关系是( )
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 不能比较 |
12.下列调查最适合用抽样调查的是( )
| A. | 某书稿中的错别字 | B. | 调查七(1)班学生的身高情况 | ||
| C. | 某品牌灯泡的使用寿命 | D. | 企业招聘,对应聘人员进行面试 |
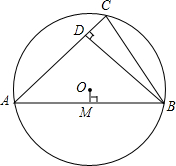 如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,OM的长为0.3,求sin∠CBD的值.
如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,OM的长为0.3,求sin∠CBD的值.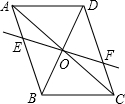 如图,在平行四边形ABCD中,对角线AC,BD交于点O,经过点O的直线交AB于E,交CD于F,
如图,在平行四边形ABCD中,对角线AC,BD交于点O,经过点O的直线交AB于E,交CD于F,