题目内容
17.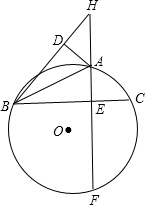 如图,△ABC内接于⊙O,AE和BD是它的两条高,相交于点H,直线AH交⊙O于点F,求证:EH=EF.
如图,△ABC内接于⊙O,AE和BD是它的两条高,相交于点H,直线AH交⊙O于点F,求证:EH=EF.
分析 连接BF,由已知条件得出∠H+∠HBE=90°,∠C+∠HBE=90°,证出∠H=∠C,由圆周角定理得出∠C=∠F,得出∠H=∠F,证出BF=BH,再由等腰三角形的三线合一性质即可得出结论.
解答 证明: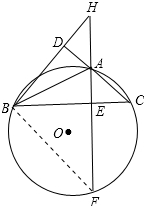 连接BF,如图所示:
连接BF,如图所示:
∵△ABC内接于⊙O,AE和BD是它的两条高,
∴∠BEH=∠BDC=90°,
∴∠H+∠HBE=90°,∠C+∠HBE=90°,
∴∠H=∠C,
又∵∠C=∠F,
∴∠H=∠F,
∴BF=BH,
又∵AE⊥BC,
∴EH=EF.
点评 本题考查了三角形的外接圆、三角形的高、圆周角定理、等腰三角形的判定与性质;通过作辅助线由圆周角定理证出∠H=∠F得出BF=BH是解决问题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 已知线段m,∠a(如图).
已知线段m,∠a(如图).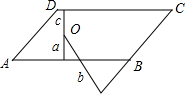 如图,在平行四边形ABCD中,AB=2AD,点O为平行四边形内一点,它到直线AB,BC,CD距离分别为a,b,c,且它到AD和CD的距离相等,则2a-b+c=0.
如图,在平行四边形ABCD中,AB=2AD,点O为平行四边形内一点,它到直线AB,BC,CD距离分别为a,b,c,且它到AD和CD的距离相等,则2a-b+c=0.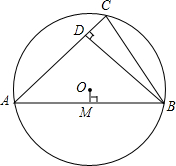 如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,OM的长为0.3,求sin∠CBD的值.
如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,OM的长为0.3,求sin∠CBD的值.