题目内容
3.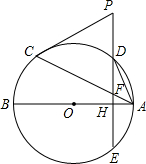 如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于E,交AB于H,交AC于F.P是ED延长线上一点且PC=PF.
如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于E,交AB于H,交AC于F.P是ED延长线上一点且PC=PF.(1)求证:PC是⊙O的切线;
(2)若点D是劣弧AC的中点,OH=1,AH=2,求弦AC的长.
分析 (1)根据等腰三角形的性质和直角三角形两锐角互余的性质,证得∠PCF+∠AC0=90°,即OC⊥PC,即可证得结论;
(2)先根据勾股定理求出DH,再通过证明△OGA≌△OHD,得出AC=2AG=2DH,求出弦AC的长.
解答 (1)证明:连接OC,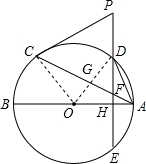
∵OA=OC,
∴∠ACO=∠OAC,
∵PC=PF,
∴∠PCF=∠PFC,
∵DE⊥AB,
∴∠OAC+∠AFH=90°,
∵∠PDF=∠AFH,
∴∠PFC+∠OAC=90°,
∴∠PCF+∠AC0=90°,
即OC⊥PC,
∴PC是⊙O的切线;
(2)解:连接OD交AC于G.
∵OH=1,AH=2,
∴OA=3,即可得OD=3,
∴DH=$\sqrt{O{D}^{2}-O{H}^{2}}$=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$.
∵点D在劣弧AC中点位置,
∴AC⊥DO,
∴∠OGA=∠OHD=90°,
在△OGA和△OHD中,
$\left\{\begin{array}{l}{∠OGA=∠OHD}\\{∠DOA=∠AOD}\\{OA=OD}\end{array}\right.$,
∴△OGA≌△OHD(AAS),
∴AG=DH,
∴AC=4$\sqrt{2}$.
点评 考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.同时考查了全等三角形的判定和性质.

练习册系列答案
相关题目
11.已知A(x1,y1)和B(x2,y2)是函数y=$\frac{{k}^{2}+1}{x}$图象上两点,当x1<x2时,y1与y2之间的大小关系是( )
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 不能确定 |
12. 如图,PA切⊙于点A,OP交⊙O于点B,且点B为OP的中点,弦AC∥OP.若OP=2,则图中阴影部分的面积为( )
如图,PA切⊙于点A,OP交⊙O于点B,且点B为OP的中点,弦AC∥OP.若OP=2,则图中阴影部分的面积为( )
 如图,PA切⊙于点A,OP交⊙O于点B,且点B为OP的中点,弦AC∥OP.若OP=2,则图中阴影部分的面积为( )
如图,PA切⊙于点A,OP交⊙O于点B,且点B为OP的中点,弦AC∥OP.若OP=2,则图中阴影部分的面积为( )| A. | $\frac{π}{3}-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{π}{3}-\frac{{\sqrt{3}}}{4}$ | C. | $\frac{π}{6}-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{π}{6}-\frac{{\sqrt{3}}}{4}$ |
 如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为73°.
如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为73°.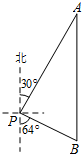 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处.海轮沿正南方向航行一段时间后,到达位于灯塔P的南偏东64°方向上的B处.求海轮所在的B处与灯塔P的距离.(结果精确到0.1海里)(参考数据:sin64°=0.90,cos64°=0.44,tan64°=2.05)
如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处.海轮沿正南方向航行一段时间后,到达位于灯塔P的南偏东64°方向上的B处.求海轮所在的B处与灯塔P的距离.(结果精确到0.1海里)(参考数据:sin64°=0.90,cos64°=0.44,tan64°=2.05)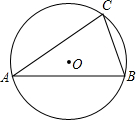 如图,△ABC内接于⊙O,∠BAC=30°,BC=$\sqrt{3}$,则⊙O的半径等于$\sqrt{3}$.
如图,△ABC内接于⊙O,∠BAC=30°,BC=$\sqrt{3}$,则⊙O的半径等于$\sqrt{3}$.