题目内容
1.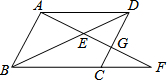 如图,平行四边形ABCD中,E是BD上一点,AE的延长线与BC的延长线交于F,与CD交于G,若AE=4,EG=3,则EF=$\frac{16}{3}$.
如图,平行四边形ABCD中,E是BD上一点,AE的延长线与BC的延长线交于F,与CD交于G,若AE=4,EG=3,则EF=$\frac{16}{3}$.
分析 由平行四边形的定义得出AB∥CD,再根据平行线的性质得到∠ABE=∠FDE,∠EAB=∠EFD,然后根据两角对应相等的两三角形相似即可证明△ABE∽△FDE;根据相似三角形对应边成比例得出$\frac{AE}{EF}=\frac{BE}{ED}$①,再证明△BEG∽△DEA,得出$\frac{BE}{ED}=\frac{EG}{AE}$②,等量代换得到$\frac{AE}{EF}=\frac{EG}{AE}$,于是得到结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABE=∠FDE,∠EAB=∠EFD,
∴△ABE∽△FDE,
∴$\frac{AE}{EF}=\frac{BE}{ED}$①,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠GBE=∠ADE,∠G=∠DEA,
∴△BEG∽△DEA,
∴$\frac{BE}{ED}=\frac{EG}{AE}$②,
由①②可得,$\frac{AE}{EF}=\frac{EG}{AE}$,
∵AE=4,EG=3,
∴EF=$\frac{16}{3}$.
故答案为:$\frac{16}{3}$.
点评 此题考查了相似三角形的判定和性质以及平行四边形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
13. 如图,一块矩形花池ABCD,AB=2$\sqrt{3}$m,AD=4m,分别以A,B,C,D为圆心,2m长为半径作四条弧交于点E,G,F,H.准备在四条弧围成的阴影区域种植紫罗兰,其余区域种植菊花,则这种紫罗兰的区域面积为( )
如图,一块矩形花池ABCD,AB=2$\sqrt{3}$m,AD=4m,分别以A,B,C,D为圆心,2m长为半径作四条弧交于点E,G,F,H.准备在四条弧围成的阴影区域种植紫罗兰,其余区域种植菊花,则这种紫罗兰的区域面积为( )
 如图,一块矩形花池ABCD,AB=2$\sqrt{3}$m,AD=4m,分别以A,B,C,D为圆心,2m长为半径作四条弧交于点E,G,F,H.准备在四条弧围成的阴影区域种植紫罗兰,其余区域种植菊花,则这种紫罗兰的区域面积为( )
如图,一块矩形花池ABCD,AB=2$\sqrt{3}$m,AD=4m,分别以A,B,C,D为圆心,2m长为半径作四条弧交于点E,G,F,H.准备在四条弧围成的阴影区域种植紫罗兰,其余区域种植菊花,则这种紫罗兰的区域面积为( )| A. | (6$\sqrt{3}$-$\frac{4}{3}$π)m2 | B. | (8$\sqrt{3}$-$\frac{4}{3}$π)m2 | C. | (6$\sqrt{3}$-$\frac{8}{3}$π)m2 | D. | (8$\sqrt{3}$-$\frac{8}{3}$π)m2 |
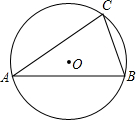 如图,△ABC内接于⊙O,∠BAC=30°,BC=$\sqrt{3}$,则⊙O的半径等于$\sqrt{3}$.
如图,△ABC内接于⊙O,∠BAC=30°,BC=$\sqrt{3}$,则⊙O的半径等于$\sqrt{3}$.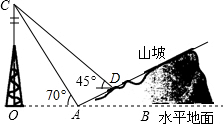 如图,小李在山坡坡脚A处测得他所在小区信号塔塔尖C的仰角为70°,在山坡上的点D处有一坐台,在点D处测得点C的仰角为45°,经侧量知信号塔塔底O距离山坡坡脚A的距离为200米,坡面的铅直高度与水平宽度的比为1:2,试根据以上数据求出信号塔塔尖:C与坐台D的距离.(结果保留整数,参考数据:cos70°≈0.34,sin70°≈0.94,tan70°≈2.75,$\sqrt{2}$=1.41)
如图,小李在山坡坡脚A处测得他所在小区信号塔塔尖C的仰角为70°,在山坡上的点D处有一坐台,在点D处测得点C的仰角为45°,经侧量知信号塔塔底O距离山坡坡脚A的距离为200米,坡面的铅直高度与水平宽度的比为1:2,试根据以上数据求出信号塔塔尖:C与坐台D的距离.(结果保留整数,参考数据:cos70°≈0.34,sin70°≈0.94,tan70°≈2.75,$\sqrt{2}$=1.41) 如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度AB长12米.
如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度AB长12米. 如图,射线OA∥BC,BO=BC,∠OBC=50°,若将射线OA绕点O顺时针方向旋转锐角x°,射线OA恰好经过点C,则x=50.
如图,射线OA∥BC,BO=BC,∠OBC=50°,若将射线OA绕点O顺时针方向旋转锐角x°,射线OA恰好经过点C,则x=50. 如图,AE∥BF,AC、BD分别是∠BAD、∠ABC的平分线,且AC交BF于点C,BD交AE于点D,连接CD.求证:四边形ABCD是菱形.
如图,AE∥BF,AC、BD分别是∠BAD、∠ABC的平分线,且AC交BF于点C,BD交AE于点D,连接CD.求证:四边形ABCD是菱形.