题目内容
18．某实验学校成立机器人兴趣小组，他们设计了一个机器人，它能根据令进行行走和旋转，某一指令规定：机器人先向前走2米，然后向左转30°，若机器人反复执行这一指令，则从出发到第一次回到原处，机器人共走了24米．分析 先判断出机器人走过的图形是正多边形，然后根据多边形的外角和等于360°求出边数，再求解即可．
解答 解：∵机器人向前走2米，然后向左转30°，反复执行这一指令，
∴从出发到第一次回到原处，机器人共走过的图形是正多边形，
边数=360°÷30°=12，
∴机器人共走了12×2=24米．
故答案为：24．
点评 本题考查了多边形的内角与外角，读懂题目信息，判断出机器人走过的图形是正多边形并求出边数是解题的关键．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
12．
如图，PA切⊙于点A，OP交⊙O于点B，且点B为OP的中点，弦AC∥OP．若OP=2，则图中阴影部分的面积为（ ）
如图，PA切⊙于点A，OP交⊙O于点B，且点B为OP的中点，弦AC∥OP．若OP=2，则图中阴影部分的面积为（ ）| A． | $\frac{π}{3}-\frac{{\sqrt{3}}}{2}$ | B． | $\frac{π}{3}-\frac{{\sqrt{3}}}{4}$ | C． | $\frac{π}{6}-\frac{{\sqrt{3}}}{2}$ | D． | $\frac{π}{6}-\frac{{\sqrt{3}}}{4}$ |
如图，某公路隧道横截面为抛物线，其最大高度为6米，底部宽度AB长12米．
13．
如图，一块矩形花池ABCD，AB=2$\sqrt{3}$m，AD=4m，分别以A，B，C，D为圆心，2m长为半径作四条弧交于点E，G，F，H．准备在四条弧围成的阴影区域种植紫罗兰，其余区域种植菊花，则这种紫罗兰的区域面积为（ ）
如图，一块矩形花池ABCD，AB=2$\sqrt{3}$m，AD=4m，分别以A，B，C，D为圆心，2m长为半径作四条弧交于点E，G，F，H．准备在四条弧围成的阴影区域种植紫罗兰，其余区域种植菊花，则这种紫罗兰的区域面积为（ ）| A． | （6$\sqrt{3}$-$\frac{4}{3}$π）m2 | B． | （8$\sqrt{3}$-$\frac{4}{3}$π）m2 | C． | （6$\sqrt{3}$-$\frac{8}{3}$π）m2 | D． | （8$\sqrt{3}$-$\frac{8}{3}$π）m2 |
如图，射线OA∥BC，BO=BC，∠OBC=50°，若将射线OA绕点O顺时针方向旋转锐角x°，射线OA恰好经过点C，则x=50．
如图，在正方形ABCD中，AB=2，分别以点A、C为圆心，以2为半径画弧，则图中阴影部分的面积是8-2π．（结果保留π）
8．
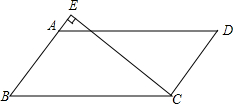如图，在平行四边形ABCD中，过点C的直线CE⊥AB，垂足为E，若∠EAD=53°，则∠BCE的度数为（ ）
如图，在平行四边形ABCD中，过点C的直线CE⊥AB，垂足为E，若∠EAD=53°，则∠BCE的度数为（ ）| A． | 53° | B． | 37° | C． | 47° | D． | 123° |