题目内容
19. 如图.抛物线y=ax2+bx+$\frac{5}{2}$与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线上位于直线AB上方的一点(不与点A,B重合),连接AD,BD.
如图.抛物线y=ax2+bx+$\frac{5}{2}$与直线AB交于点A(-1,0),B(4,$\frac{5}{2}$),点D是抛物线上位于直线AB上方的一点(不与点A,B重合),连接AD,BD.(1)求抛物线的解析;
(2)设△ADB的面为S,求出当S取最大值时的点D的坐标.
分析 (1)把A、B两点坐标代入抛物线解析式即可.
(2)设点D坐标为(m,-$\frac{1}{2}$m2+2m+$\frac{5}{2}$),直线DC⊥x轴,与AB交于点C,根据S△ABD=S△ACD+S△BCD构建二次函数,利用二次函数的最值问题解决.
解答 解:(1)∵抛物线y=ax2+bx+$\frac{5}{2}$经过点A(-1,0),B(4,$\frac{5}{2}$),
∴$\left\{\begin{array}{l}{a-b+\frac{5}{2}=0}\\{16a+4b+\frac{5}{2}=\frac{5}{2}}\end{array}\right.$解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴抛物线解析式为y=-$\frac{1}{2}$x2+2x+$\frac{5}{2}$.
(2)设点D坐标为(m,-$\frac{1}{2}$m2+2m+$\frac{5}{2}$),直线DC⊥x轴,与AB交于点C,
∵直线AB解析式为y=$\frac{1}{2}$x+$\frac{1}{2}$,
∴点C坐标(m,$\frac{1}{2}$m+$\frac{1}{2}$),
∵S△ABD=S△ACD+S△BCD=$\frac{1}{2}$(-$\frac{1}{2}$m2+2m+$\frac{5}{2}$-$\frac{1}{2}$m-$\frac{1}{2}$)×(4+1)=-$\frac{5}{4}$(m2-3m-4)=-$\frac{5}{4}$(m-$\frac{3}{2}$)2+$\frac{125}{16}$,
∴当m=$\frac{3}{2}$时,△ADB面积最大,此时点D坐标($\frac{3}{2}$,$\frac{35}{8}$).
点评 本题考查二次函数的最值、一次函数等知识,解题的关键是掌握待定系数法确定函数解析式,学会构建二次函数,利用二次函数的性质解决问题,属于中考常考题型.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案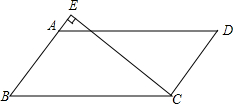 如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为( )
如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为( )| A. | 53° | B. | 37° | C. | 47° | D. | 123° |
 如图,射线OA∥BC,BO=BC,∠OBC=50°,若将射线OA绕点O顺时针方向旋转锐角x°,射线OA恰好经过点C,则x=50.
如图,射线OA∥BC,BO=BC,∠OBC=50°,若将射线OA绕点O顺时针方向旋转锐角x°,射线OA恰好经过点C,则x=50. 如图,在正方形ABCD中,AB=2,分别以点A、C为圆心,以2为半径画弧,则图中阴影部分的面积是8-2π.(结果保留π)
如图,在正方形ABCD中,AB=2,分别以点A、C为圆心,以2为半径画弧,则图中阴影部分的面积是8-2π.(结果保留π) 如图所示的图案绕点O顺时针旋转,至少旋转120°后,与原来的图案重合.
如图所示的图案绕点O顺时针旋转,至少旋转120°后,与原来的图案重合. 如图,AE∥BF,AC、BD分别是∠BAD、∠ABC的平分线,且AC交BF于点C,BD交AE于点D,连接CD.求证:四边形ABCD是菱形.
如图,AE∥BF,AC、BD分别是∠BAD、∠ABC的平分线,且AC交BF于点C,BD交AE于点D,连接CD.求证:四边形ABCD是菱形.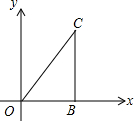 如图,在Rt△OBC中,OB与x轴正半轴重合,∠OBC=90°,且OC=2,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC,得到△OB2C2,…,如此继续下去,得到△OB2016C2016,则点C2016的坐标为(22016,$\sqrt{3}$•22016).
如图,在Rt△OBC中,OB与x轴正半轴重合,∠OBC=90°,且OC=2,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC,得到△OB2C2,…,如此继续下去,得到△OB2016C2016,则点C2016的坐标为(22016,$\sqrt{3}$•22016).