Question

11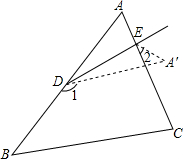．如图所示，将纸片△ABC沿DE折叠，点A落在点A′处，已知∠1=140°，∠2=40°，求∠A的度数．

Answer 1

分析 先根据图形翻折变换的性质得出∠ADE的度数，再由三角形外角的性质可知∠DEC=∠A+∠ADE，根据三角形内角和定理即可得出结论．

解答 解：∵∠1=140°，
∴∠ADA′=40°．
∵∠ADE=∠EAD′=20°，
∴∠DEC=∠A+20°．
∵∠DEC+∠2=∠DEA=180°-∠A-20°，
∴∠A+20°+40°=180°-∠A-20°，
∴∠A=50°．

点评 本题考查的是三角形定理，熟知三角形内角和是180°是解答此题的关键．