题目内容
2.已知有理数a、b满足($\sqrt{6}$+7)a+2$\sqrt{6}$=($\sqrt{6}$-7)b,求a2+b2的值.分析 已知等式整理后,确定出a与b的值,代入原式计算即可得到结果.
解答 解:已知等式整理得:(a+2)$\sqrt{6}$+7a=$\sqrt{6}$b-7b,
可得$\left\{\begin{array}{l}{a+2=b}\\{7a=-7b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=1}\end{array}\right.$,
则原式=1+1=2.
点评 此题考查了实数的运算,以及解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
14.为了解某县八年级9800名学生的视力情况,从中抽查了100名学生的视力情况,对于这个问题,下面说法中正确的是( )
| A. | 9800名学生是总体 | |
| B. | 每个学生是个体 | |
| C. | 100名学生是所抽取的一个样本 | |
| D. | 100名学生的视力情况是所抽取的一个样本 |
12.如图①,把∠α=60°的一个单独的菱形称作一个基本图形,将此基本图形不断的复制并平移,使得下一个菱形的一个顶点与前一个菱形的中心重合,这样得到图②,图③,…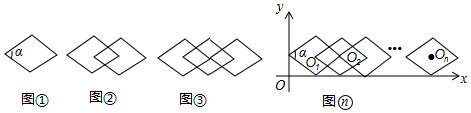
(1)观察图形并完成表格:
猜想:在图n中,菱形的个数为4n-5[用含有n(n≥3)的代数式表示];
(2)如图,将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(x1,1),则x1=$\sqrt{3}$;第2017个基本图形的中心O2017的坐标为(2017$\sqrt{3}$,1).

(1)观察图形并完成表格:
| 图形名称 | 基本图形的个数 | 菱形的个数 |
| 图① | 1 | 1 |
| 图② | 2 | 3 |
| 图③ | 3 | 7 |
| 图④ | 4 | 11 |
| … | … | … |
(2)如图,将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(x1,1),则x1=$\sqrt{3}$;第2017个基本图形的中心O2017的坐标为(2017$\sqrt{3}$,1).
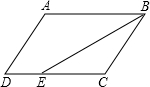 如图,在?ABCD中,已知AB=11cm,AD=5cm,BE平分∠ABC交DC边于点E,求DE的长.
如图,在?ABCD中,已知AB=11cm,AD=5cm,BE平分∠ABC交DC边于点E,求DE的长. 如图,将一张长形纸片ABCD沿着EF折叠,若∠EFG=36°,试求∠BGE的度数?
如图,将一张长形纸片ABCD沿着EF折叠,若∠EFG=36°,试求∠BGE的度数? 如图,AB是⊙O的弦,BC与⊙O相切于点B,连接OA,OB,若∠ABC=65°,则∠AOB等于130°.
如图,AB是⊙O的弦,BC与⊙O相切于点B,连接OA,OB,若∠ABC=65°,则∠AOB等于130°.