题目内容
11. 如图,AB是⊙O的弦,BC与⊙O相切于点B,连接OA,OB,若∠ABC=65°,则∠AOB等于130°.
如图,AB是⊙O的弦,BC与⊙O相切于点B,连接OA,OB,若∠ABC=65°,则∠AOB等于130°.
分析 根据切线的性质得到∠OBC=90°,求出∠ABO和∠OAB,根据三角形内角和定理计算即可.
解答 解:∵BC与⊙O相切于点B,
∴∠OBC=90°,
∴∠ABO=90°-65°=25°,
∵OA=OB,
∴∠OAB=∠ABO=25°,
∴∠AOB=180°-25°×2=130°,
故答案为:130°.
点评 本题考查的是切线的性质、三角形内角和定理的应用,掌握圆的切线垂直于经过切点的半径是解题的关键.

练习册系列答案
相关题目
1.在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当m≥10时为A级,5≤m<10时为B级,当0≤m<5为C级.现随机抽取30个符合年龄条件的青年人开展“每人日均发微博条数”的调查,所有抽青年人的“日均发微博条数”的数据如表:
(1)求样本数据中为A级的频率;
(2)试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数;
(3)从样本数据为C级的人中随机抽取两人,用列举法求抽得两个人的“日均发微博条数”都是3的概率.
| 11 | 10 | 6 | 15 | 9 | 16 | 13 | 12 | 0 | 8 | 2 | 8 | 10 | 17 | 6 |
| 13 | 7 | 5 | 7 | 3 | 12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
(2)试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数;
(3)从样本数据为C级的人中随机抽取两人,用列举法求抽得两个人的“日均发微博条数”都是3的概率.
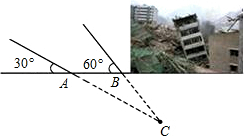 由于发生山体滑坡灾害,武警救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧地面上探测点A、B相距2米,探测线与该地面的夹角分别是30°和60°(如图所示),试确定生命所在点C的深度.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$,1.732,结果精确到0.1)
由于发生山体滑坡灾害,武警救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧地面上探测点A、B相距2米,探测线与该地面的夹角分别是30°和60°(如图所示),试确定生命所在点C的深度.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$,1.732,结果精确到0.1)