题目内容
12.如果∠A和∠B的两边分别互相平行,且满足∠B=4∠A-30°,则∠A 的度数是42°或10°.分析 由∠A与∠B的两边分别平行,即可得∠A与∠B相等或互补,然后分两种情况,分别根据∠A与∠B相等或互补,即可求得∠A的度数.
解答 解:∵∠A与∠B的两边分别平行,
∴∠A与∠B相等或互补.
分两种情况:
①当∠A+∠B=180°时,
由∠B=4∠A-30°可得,∠A+4∠A-30°=180°,
解得:∠A=42°;
②当∠A=∠B时,
由∠B=4∠A-30°可得,∠A=4∠A-30°,
解得:∠A=10°.
所以∠A=42°或10°.
故答案为:42°或10°.
点评 此题考查的是平行线的性质,解题时注意:如果两角的两边分别平行,则这两个角相等或互补.

练习册系列答案
相关题目
2.若2011a+2012b=0,则ab是( )
| A. | 正数 | B. | 非正数 | C. | 负数 | D. | 非负数 |
7.某工厂计划招聘A、B两个工种的工人共120人,A、B两个工种的工人月工资分别为1600元和2000元.
(1)若某工厂每月支付的工人工资为220000元,那么A、B两个工种的工人各招聘多少人?设招聘A工种的工人x人,根据题设完成下列表格,并列方程求解
(2)设工厂每月支付的工人工资y元,试写出y与x之间的函数表达式,若要求B工种的人数不少于A工种人数的2倍,那么招聘A工种的工人多少人时,可使工厂每月支付的工人工资最少?
(1)若某工厂每月支付的工人工资为220000元,那么A、B两个工种的工人各招聘多少人?设招聘A工种的工人x人,根据题设完成下列表格,并列方程求解
(2)设工厂每月支付的工人工资y元,试写出y与x之间的函数表达式,若要求B工种的人数不少于A工种人数的2倍,那么招聘A工种的工人多少人时,可使工厂每月支付的工人工资最少?
| 工种 | 工人每月工资(元) | 招聘人数 | 工厂应付工人的约工资(元) |
| A | 1600 | x | 1600x |
| B | 2000 | 120-x | 2000(120-x) |
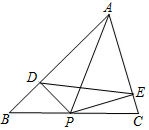 如图,在△ABC中,∠B=45°,∠C=75°,BC=6-2$\sqrt{3}$,点P是BC上一动点,PD⊥AB于D,PE⊥AC于E,则线段DE的最小值为$\sqrt{3}$.
如图,在△ABC中,∠B=45°,∠C=75°,BC=6-2$\sqrt{3}$,点P是BC上一动点,PD⊥AB于D,PE⊥AC于E,则线段DE的最小值为$\sqrt{3}$.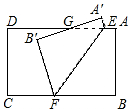 如图,把长方形纸片ABCD沿EF折叠,点A、B分别落在A′、B′处.A′B′与AD交于点G,若∠CFB′=50°,则∠AEF=115°.
如图,把长方形纸片ABCD沿EF折叠,点A、B分别落在A′、B′处.A′B′与AD交于点G,若∠CFB′=50°,则∠AEF=115°.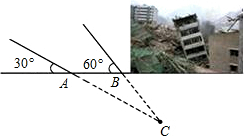 由于发生山体滑坡灾害,武警救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧地面上探测点A、B相距2米,探测线与该地面的夹角分别是30°和60°(如图所示),试确定生命所在点C的深度.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$,1.732,结果精确到0.1)
由于发生山体滑坡灾害,武警救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧地面上探测点A、B相距2米,探测线与该地面的夹角分别是30°和60°(如图所示),试确定生命所在点C的深度.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$,1.732,结果精确到0.1)