题目内容
9.已知二次函数y=x2-kx+k-1(k>2).(1)求证:抛物线y=x2-kx+k-1(k>2)与x轴必有两个交点;
(2)抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,若tan∠OAC=3,求抛物线的表达式.
分析 (1)先计算判别式的值得到△=(k-2)2,利用k>2,可判断△>0,于是根据△=b2-4ac>0时,抛物线与x轴有2个交点即可得到结论;
(2)根据抛物线与x轴的交点问题,解方程x2-kx+k-1=0得x=k-1或x=1,利用k>2,点A在点B的左侧得到A(1,0),B(k-1,0),再表示出C(0,k-1),然后根据正切的定义得到$\frac{k-1}{1}$=3,再解方程求出k即可得到抛物线的表达式.
解答 (1)证明:∵△=(-k)2-4×1×(k-1)=(k-2)2,
又∵k>2,
∴(k-2)2>0,即△>0.
∴抛物线y=x2-kx+k-1与x轴必有两个交点;
(2)解:∵抛物线y=x2-kx+k-1与x轴交于A、B两点,
∴令y=0,有x2-kx+k-1=0,解得x=k-1或x=1,
∵k>2,点A在点B的左侧,
∴A(1,0),B(k-1,0),
∵抛物线与y轴交于点C,
∴C(0,k-1),
在Rt△AOC中,∵tan∠OAC=$\frac{OC}{OA}$=3,
∴$\frac{k-1}{1}$=3,解得k=4.
∴抛物线的表达式为y=x2-4x+3.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程;△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.也考查了三角函数的定义.

练习册系列答案
相关题目
14.抛物线y=2(x-1)2的对称轴是( )
| A. | 1 | B. | 直线x=1 | C. | 直线x=2 | D. | 直线x=-1 |
19.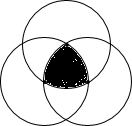 如图,分别以边长为2的正三角形的顶点为圆心,2为半径作三个圆,则这三个圆围成的阴影部分面积是( )
如图,分别以边长为2的正三角形的顶点为圆心,2为半径作三个圆,则这三个圆围成的阴影部分面积是( )
 如图,分别以边长为2的正三角形的顶点为圆心,2为半径作三个圆,则这三个圆围成的阴影部分面积是( )
如图,分别以边长为2的正三角形的顶点为圆心,2为半径作三个圆,则这三个圆围成的阴影部分面积是( )| A. | 2π | B. | 2π-$\sqrt{3}$ | C. | 2π-2$\sqrt{3}$ | D. | 2π-3$\sqrt{3}$ |
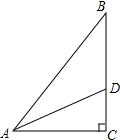 如图,在△ABC中,∠C=90°,BC=12,AD平分∠BAC,且AD=8,则△ABC的面积等于24$\sqrt{3}$.
如图,在△ABC中,∠C=90°,BC=12,AD平分∠BAC,且AD=8,则△ABC的面积等于24$\sqrt{3}$.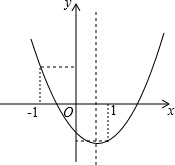 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①点(-ab,c)在第四象限;②a+b+c<0;③$\frac{a+c}{b}$>1;④2a+b>0.其中正确的是①②④.(把所有正确结论的序号都选上)
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①点(-ab,c)在第四象限;②a+b+c<0;③$\frac{a+c}{b}$>1;④2a+b>0.其中正确的是①②④.(把所有正确结论的序号都选上)