题目内容
19.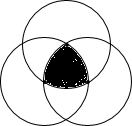 如图,分别以边长为2的正三角形的顶点为圆心,2为半径作三个圆,则这三个圆围成的阴影部分面积是( )
如图,分别以边长为2的正三角形的顶点为圆心,2为半径作三个圆,则这三个圆围成的阴影部分面积是( )| A. | 2π | B. | 2π-$\sqrt{3}$ | C. | 2π-2$\sqrt{3}$ | D. | 2π-3$\sqrt{3}$ |
分析 连接三个圆的交点可得到△ABC,由于每个圆必过另一个圆的圆心,所以△ABC即为边长为2的等边三角形,故S阴影=3S扇形ABC-2S△ABC,由此可得出结论、
解答 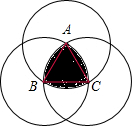 解:连接三个圆的交点可得到△ABC,
解:连接三个圆的交点可得到△ABC,
∵分别以边长为2的正三角形的顶点为圆心,2为半径作三个圆,
∴每个圆必过另一个圆的圆心,
∴△ABC即为边长为2的等边三角形,
∴S阴影=3S扇形ABC-2S△ABC
=3×$\frac{60π×{2}^{2}}{360}$-2×$\frac{1}{2}$×2×2sin60°
=2π-2$\sqrt{3}$.
故选C.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
相关题目
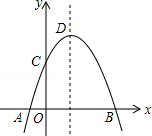 如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题: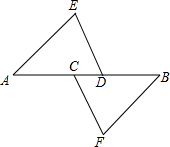 已知:如图,C、D在AB上,且AC=BD,AE∥FB,DE∥FC.求证:AE=BF.
已知:如图,C、D在AB上,且AC=BD,AE∥FB,DE∥FC.求证:AE=BF.