题目内容
9.某药材种植户经销一种药材,已知这种药材的成本价为每千克20元,经市场调查发现,该药材每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=-x+60.设这种药材每天的销售利润为w元.(1)求w与x之间的函数关系式.
(2)如果物价部门规定这种药材的销售价每千克不高于48元,该药材种植户想要每天获得300元的销售利润,销售价应定为每千克多少元?
(3)能否获得比300元更大的利润?如果能,请求出销售单价和最大利润;如果不能,请说明埋由.
分析 (1)每天的销售利润W=每天的销售量×每件产品的利润;
(2)根据题意列方程即可得到结论;
(3)根据(1)得到的函数关系式求得相应的最值问题即可.
解答 解:(1)y=(-x+60)(x-20)=-x2+20x+60x-1200=-x2+80x-1200;
(2)根据题意得:(-x+60)(x-20)=300,
解得:x1=50>48(不合题意,舍去),x2=30,
答:该药材种植户想要每天获得300元的销售利润,销售价应定为每千克30元,;
(3)能获得比300元更大的利润,
由y=-x2+80x-1200得:
y=-(x2-80x+1200)
=-(x2-80x+402-402+1200)
=-[(x-40)2-400]
=-(x-40)2+400
当x=40时,y有最大值,其最大值为400.
答:销售价定为40元时,每天的销售利润最大,最大利润是400元.
点评 本题考查了二次函数的应用;得到每天的销售利润的关系式是解决本题的关键;利用配方法或公式法求得二次函数的最值问题是常用的解题方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.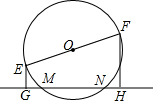 如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )
如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )
 如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )
如图,EF为⊙O的直径,EF=10cm,弦NN=6cm,则E、F两点到直线MN的距离之和等于( )| A. | 12cm | B. | 8cm | C. | 6cm | D. | 3cm |
 如图所示,点O在直线AC上,过O点作射线OB,请画出∠COB的平分线OF和∠AOB的平分线OE,求∠EOF的度数.
如图所示,点O在直线AC上,过O点作射线OB,请画出∠COB的平分线OF和∠AOB的平分线OE,求∠EOF的度数.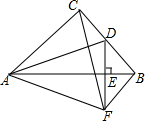 如图所示,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连结CF、AD.
如图所示,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连结CF、AD.