题目内容
4.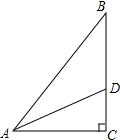 如图,在△ABC中,∠C=90°,BC=12,AD平分∠BAC,且AD=8,则△ABC的面积等于24$\sqrt{3}$.
如图,在△ABC中,∠C=90°,BC=12,AD平分∠BAC,且AD=8,则△ABC的面积等于24$\sqrt{3}$.
分析 作DE⊥AB于E,设CD=x,根据勾股定理列出关于x的方程,解方程求出CD,根据勾股定理求出AC,根据三角形面积公式计算即可.
解答 解: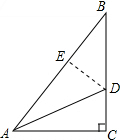 作DE⊥AB于E,
作DE⊥AB于E,
设CD=x,
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴DE=CD=x,
由勾股定理得,AC=$\sqrt{64-{x}^{2}}$,
则AE=$\sqrt{64-{x}^{2}}$,
BE=$\sqrt{(12-x)^{2}-{x}^{2}}$,
∴$(\sqrt{64-{x}^{2}}+\sqrt{144-24x})^{2}$=64-x2+144,
解得,x=4,x=4±4$\sqrt{7}$(不合题意舍去),
当CD=4时,AC=$\sqrt{64-{x}^{2}}$=4$\sqrt{3}$,
∴△ABC的面积=$\frac{1}{2}$×AC×CB=24$\sqrt{3}$,
故答案为:24$\sqrt{3}$.
点评 本题考查的是角平分线的性质和勾股定理的应用,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.下列说法正确的是( )
| A. | 对应边都成正比例的多边形相似 | B. | 对应角都相等的多边形相似 | ||
| C. | 等边三角形都相似 | D. | 矩形都相似 |
 如图所示,点O在直线AC上,过O点作射线OB,请画出∠COB的平分线OF和∠AOB的平分线OE,求∠EOF的度数.
如图所示,点O在直线AC上,过O点作射线OB,请画出∠COB的平分线OF和∠AOB的平分线OE,求∠EOF的度数.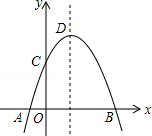 如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题: