题目内容
1.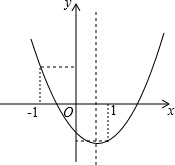 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①点(-ab,c)在第四象限;②a+b+c<0;③$\frac{a+c}{b}$>1;④2a+b>0.其中正确的是①②④.(把所有正确结论的序号都选上)
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①点(-ab,c)在第四象限;②a+b+c<0;③$\frac{a+c}{b}$>1;④2a+b>0.其中正确的是①②④.(把所有正确结论的序号都选上)
分析 ①根据抛物线的开口可确定a的符号,根据抛物线的对称轴的位置可确定b的符号,根据抛物线与y的交点的位置可确定c的符号,从而得到-ab的符号,即可确定点(-ab,c)所在的象限;
②结合图象即可得到x=1时y=a+b+c的符号;
③结合图象可得x=-1时y=a-b+c的符号,再结合b<0就可解决问题;
④结合图象可得x=-$\frac{b}{2a}$<1,再结合a>0就可解决问题.
解答 解:①由抛物线的开口向上可得a>0,
由抛物线的对称轴在y轴的右侧可得x=-$\frac{b}{2a}$>0,则b<0,
由抛物线与y的交点在y轴的负半轴可得c<0,
则有-ab>0,
因而点(-ab,c)在第四象限;
②结合图象可得,当x=1时y=a+b+c<0;
③结合图象可得,当x=-1时y=a-b+c>0,即a+c>b,
∵b<0,∴$\frac{a+c}{b}$<1;
④结合图象可得,x=-$\frac{b}{2a}$<1,
∵a>0,∴-b<2a,即2a+b>0.
故答案为①②④.
点评 本题主要考查了抛物线的性质(开口、对称轴等)、抛物线上点的坐标特征等知识,运用数形结合的思想是解决本题的关键.

练习册系列答案
相关题目
16.下列说法正确的是( )
| A. | 对应边都成正比例的多边形相似 | B. | 对应角都相等的多边形相似 | ||
| C. | 等边三角形都相似 | D. | 矩形都相似 |
 小明家有一块三角形的玻璃不小心打破了如图所示,现在要带其中一块碎片去玻璃店配一块和原来形状、大小一样的玻璃,应该带③.(填序号①、②、③)
小明家有一块三角形的玻璃不小心打破了如图所示,现在要带其中一块碎片去玻璃店配一块和原来形状、大小一样的玻璃,应该带③.(填序号①、②、③)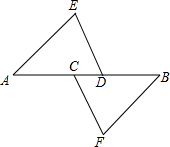 已知:如图,C、D在AB上,且AC=BD,AE∥FB,DE∥FC.求证:AE=BF.
已知:如图,C、D在AB上,且AC=BD,AE∥FB,DE∥FC.求证:AE=BF.