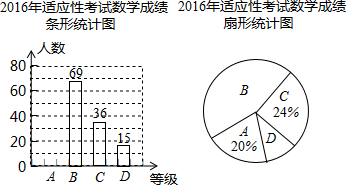
题目内容
20.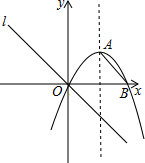 如图,抛物线y=ax2+2x与x轴交于点B,其对称轴为x=3.
如图,抛物线y=ax2+2x与x轴交于点B,其对称轴为x=3.(1)求a的值和顶点A的坐标;
(2)过点O作直线l,使l∥AB,点P是l上一动点,设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为t,当0<S≤18时,求t的取值范围.
(3)在(2)的条件下,当t取最大值时,抛物线上是否存在点Q,使△OPQ为直角三角形且OP为直角边,若存在,直接写出点Q的坐标;若不存在,说明理由.
分析 (1)先依据抛物线的对称性得到B(6,0),将点B的坐标代入抛物线的解析式可求得a的值,从而得到抛物线的解析式,将点A的横坐标代入可求得点A的纵坐标;
(2)先利用待定系数法求得直线AB的解析式,从而得到直线l的解析式,于是得到点P坐标为(t,-t).当点P在第四象限时,由S=S△ABO+S△OBP得到S与t的函数关系,然后由S的取值范围可求得t的范围;当点P在第二象限时,(t<0),过点P作PM⊥x轴,垂足为M,由S=S梯形ANMP-S△PMO+S△ABN得到S与t的关系式,从而可求得t的取值范围;
(3)由(2)可知t的最大值为3,于是可求得点P的坐标,分别过点O和点P作l的垂线,交抛物线与点Q1、Q2、Q3,接下来,求得OQ3、Q1Q2的解析式,最后将直线与抛物线的解析式联立可解得点Q1、Q2、Q3的坐标.
解答 解:(1)∵点B与点O关于x=3对称,
∴B(6,0).
∴36a+12=0,解得a=-$\frac{1}{3}$.
∴抛物线的解析式为y=-$\frac{1}{3}$x2+2x.
当x=3时,y=-$\frac{1}{3}$×9+2×3=3.
∴顶点A的坐标为(3,3).
(2)设直线AB的解析式为y=kx+b.
∵A(3,3),B(6,0),
∴$\left\{\begin{array}{l}{6k+b=0}\\{3k+b=3}\end{array}\right.$,解得:k=1,b=6.
∴直线AB的解析式为y=-x+6.
∵直线l与AB平行,
∴直线l的解析式为y=-x.
∵点P是l上一动点且横坐标为t,
∴点P坐标为(t,-t).
当点P在第四象限时,(t>0)如图1所示.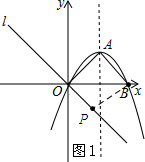
S=S△ABO+S△OBP=$\frac{1}{2}$×6×3+$\frac{1}{2}$×6×t=9+3t.
∵0<S≤18,
∴0<9+3t≤18.
∴-3<t≤3.
又∵t>0,
∴0<t≤3.
当点P在第二象限时,(t<0),如图2所示:过点P作PM⊥x轴,垂足为M.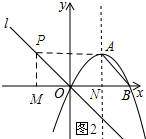
S=S梯形ANMP-S△PMO+S△ABN=$\frac{1}{2}$(3-t)(3-t)-$\frac{1}{2}$×(-t)×(-t)+$\frac{1}{2}$×3×3=-3t+9.
∵0<S≤18,
∴0<-3t+9≤18.
∴-3≤t<3.
又∵t<0,
∴-3≤t<0.
综上所述,t的取值范围是-3≤t<0或0<t≤3.
(3)当t=3时,点P的坐标为(3,-3).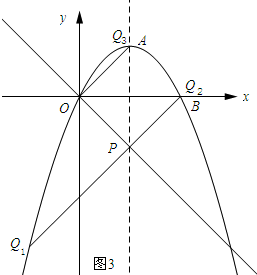
如图3所示:过点P作Q1Q2⊥OP,交抛物线与Q1,Q2两点,过点O作OQ3⊥OP交抛物线与Q3.
∵直线l的解析式为y=-x,
∴直线OA的解析式y=x.
将y=x与y=-$\frac{1}{3}$x2+2x联立得:$\left\{\begin{array}{l}{y=x}\\{y=-\frac{1}{3}{x}^{2}+2x}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$(舍去)
∴Q3的坐标为(3,3).
设Q1Q2的解析式为y=x+b,将点P的坐标代入得:3+b=-3,
解得b=-6,
∴直线Q1Q2的解析式为y=x-6.
将y=x-6与y=-$\frac{1}{3}$x2+2x联立得$\left\{\begin{array}{l}{y=x-6}\\{y=-\frac{1}{3}{x}^{2}+2x}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-3}\\{y=-9}\end{array}\right.$或$\left\{\begin{array}{l}{x=6}\\{y=0}\end{array}\right.$.
∴Q1(-3,-9),Q2(6,0).
综上所述点Q的坐标为(3,3)或(-3,-9)或(6,0).
点评 本题主要考查的是二次函数的应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式,不规则图形的面积、直线与抛物线的交点,得到S与t的函数关系式是解答问题(2)的关键,求得直线OQ3、Q1Q2的解析式是解答问题(3)的关键.

| A. | 整数 | B. | 非负数 | C. | 正数 | D. | 无法确定 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |