题目内容
5.我校为开展研究性学习,准备购买一定数量的两人学习桌和三人学习桌,若购买1张两人学习桌,1张三人学习桌需230元;若购买2张两人学习桌,3张三人学习桌需590元.(1)求两人学习桌和三人学习桌的单价;
(2)学校欲投入资金不超过6600元,购买两种学习桌共60张,以至少满足137名学生的需求,有几种购买方案?并求哪种购买方案费用最低?
分析 (1)设两人学习桌和三人学习桌的单价分别是x元、y元,然后列出二元一次方程组,求解即可;
(2)表示出三人桌的张数,然后根据资金和学生数列出不等式组,再求解得到m的取值范围,再根据资金=两人桌和三人桌的费用之和列式整理即可得解;
解答 解:(1)设两人桌每张x元,三人桌每张y元,
根据题意得,$\left\{\begin{array}{l}{x+y=230}\\{2x+3y=590}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=100}\\{y=120}\end{array}\right.$;
(2)设两人桌m张,则三人桌(60-m)张,
根据题意可得$\left\{\begin{array}{l}{2m+3(60-m)≥137}\\{100m+130(60-m)≤6600}\end{array}\right.$,
解得 40≤m≤43
m为正整数,m为40、41、42、43 共有4种方案
设费用为W
W=100m+130(60-m)=-30m+7800
m=43时,W最小为6510元.
点评 本题考查了一次函数的应用,二元一次方程组的应用,一元一次不等式组的应用,求出m的取值范围是解题的关键.

练习册系列答案
相关题目
4.用“代入消元法”解方程组$\left\{\begin{array}{l}y=2-x\\ 2x-3y=19.\end{array}\right.$时,①代入②正确的是( )
| A. | 2x-6+3x=19 | B. | 2x-6-3x=19 | C. | 2x-6+x=19 | D. | 2x-6-x=19 |
17.以下问题不适合用全面调查的是( )
| A. | 了解光明中学901班同学每周体育锻炼的时间 | |
| B. | 安踏鞋厂生产的鞋底能承受的弯折次数 | |
| C. | 咸丰民中招聘教师,对应聘人员面试 | |
| D. | 调查光明中学683名学生的身高 |
14.某中学随机抽取了该校50名学生,他们的年龄如表所示:
这50名学生年龄的众数和中位数分别是( )
| 年龄(单位:岁) | 12 | 13 | 14 | 15 |
| 人数 | 12 | 14 | 18 | 6 |
| A. | 13岁、14岁 | B. | 14岁,14岁 | C. | 14岁,13岁 | D. | 14岁,15岁 |
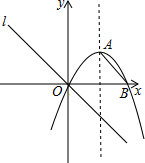 如图,抛物线y=ax2+2x与x轴交于点B,其对称轴为x=3.
如图,抛物线y=ax2+2x与x轴交于点B,其对称轴为x=3.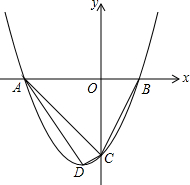 已知:二次函数y=ax2+bx+c的图象与x轴相交于A(-4,0),B(2,0)两点,与y轴相交于点C(0,-4),点D为抛物线的顶点.
已知:二次函数y=ax2+bx+c的图象与x轴相交于A(-4,0),B(2,0)两点,与y轴相交于点C(0,-4),点D为抛物线的顶点.