题目内容

11．对于任意的实数x，代数式x2-3x+3的值是一个（　　）
A．整数B．非负数C．正数D．无法确定

分析 根据完全平方公式，将x2-3x38转化为完全平方的形式，再进一步判断．

解答 解：多项式x2-3x+3变形得x2-3x+$\frac{9}{4}$+$\frac{3}{4}$=（x-$\frac{3}{2}$）2+$\frac{3}{4}$，
任意实数的平方都是非负数，其最小值是0，
所以（x-$\frac{3}{2}$）2+$\frac{3}{4}$的最小值是$\frac{3}{4}$，
故多项式x2-3x+3的值是一个正数，
故选C．

点评 本题考查了配方法的应用，任意实数的平方和绝对值都具有非负性，灵活运用这一性质是解决此类问题的关键．

练习册系列答案
相关题目
10．将纸片△ABC沿AD折叠，使C点刚好落在AB边上的E处，展开如图（1）．

【操作观察】（1）作DF⊥AC，且DF=3，AB=8，则S△ABD=12；
【理解运用】如图（2）若∠BAC=60°，AC=8，F是AC的中点，连接EF交AD于点M，点P是AD上的动点，连接PF和PC，试说明：PF+PC≥$4\sqrt{3}$；
【拓展提高】请根据前面的解题经验，解决下面问题：如图（3），在平面直角坐标系中，A点的坐标为（1，3），B点的坐标为（3，-2），点P是x轴上的动点，连接AP、BP，求AP-BP的最大值，并写出P点的坐标．
11．下列式子中，是一元一次方程的是（　　）
A．3x+1=4xB．x+2＞1C．x2-9=0D．2x-3y=0
8．由38位科学家通过云计算得出：现在地球上约有3040000000000棵存活的树，将3040000000000用科学记数法表示为3.04×1012．
6．甲、乙两地之间的公路长120千米，一辆汽车从甲地匀速驶往乙地，比原计划晚出发24分钟，该车实际行驶的速度是原计划行驶的速度的1.25倍，结果按原计划时间到达乙地，求该车实际行驶速度．
16．某学校将“阳光体育”项目定为跳绳活动，为此学校准备购置长、短两种跳绳若干．若购买30条长跳绳和20条短跳绳共需720元，且购买10条长跳绳比12条短跳绳多花16元．
（1）两种跳绳的单价各是多少元？
（2）若学校一次性购买长、短跳绳共200条，要使总费用不超过3000元，最少可购买多少条短跳绳？
3．哈市松北区教育局为鼓励先进、倡导绿色出行，组织骑行大赛，并未参赛的部分优秀学生选手购买骑行帽，按原价用规划的2400元可购买这种骑行帽若干个，商场老板也是个自行车运动爱好者，得知情况后，决定给予八折优惠，结果教育局用这规划的2400元购买的骑行帽数量比按原价购买多四个．
（1）求这种骑行帽原价多少元一个？
（2）由于宣传到位，参赛同学增多，教育局准备再追加购奖款10000元，用于购买这种骑行帽和防霾口罩共200个，用于奖励参赛学生，商场老板调取订货单查出骑行帽进价80元/个，防霾口罩进价10元/个，商场老板与教育局协商后将防霾口罩按利润率20%的价格出售，骑行帽仍可按八折购买，则教育局用追加购奖款最多可购买多少个骑行帽？
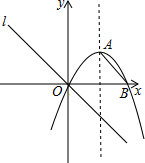20．如图，抛物线y=ax2+2x与x轴交于点B，其对称轴为x=3．
（1）求a的值和顶点A的坐标；
（2）过点O作直线l，使l∥AB，点P是l上一动点，设以点A、B、O、P为顶点的四边形面积为S，点P的横坐标为t，当0＜S≤18时，求t的取值范围．
（3）在（2）的条件下，当t取最大值时，抛物线上是否存在点Q，使△OPQ为直角三角形且OP为直角边，若存在，直接写出点Q的坐标；若不存在，说明理由．
1．方程2x+1=5的解是（　　）
A．2B．-2C．3D．-3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网