题目内容
16.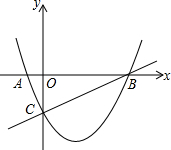 如图:已知抛物线y=ax2-$\frac{3}{2}$x+c与x轴相交于A、B两点,并与直线y=$\frac{1}{2}$x-2交于B、C两点,其中点C是直线y=$\frac{1}{2}$x-2与y轴交点,连接AC,
如图:已知抛物线y=ax2-$\frac{3}{2}$x+c与x轴相交于A、B两点,并与直线y=$\frac{1}{2}$x-2交于B、C两点,其中点C是直线y=$\frac{1}{2}$x-2与y轴交点,连接AC,(1)求抛物线解析式;
(2)证明:△ABC为直角三角形;
(3)在抛物线CB段上存在点P使得以A,C,P,B为顶点的四边形面积最大,请求出点P的坐标以及此时以A,C,P,B为顶点的四边形面积.
分析 (1)由直线y=$\frac{1}{2}$x-2交x轴、y轴于点B、C两点可求得点B和点C的坐标,然后将点B和点C的坐标代入抛物线的解析式得到关于a、c的方程组,从而可求得a、c的值;
(2)先求得点A和点B的坐标,然后依据勾股定理可求得AC和BC的长,最后依据勾股定理的逆定理可证明△ABC为直角三角形;
(3)设出点P与点D的坐标,可求得PD的长(用含a的式子表示),依据二次函数的性质可知当a=2时,PD的最大值为2,由三角形的面积公式可知DP有最大值时,△BCD的面积最大,由于△ABC的面积为定值,故此时四边形ACPB的面积最大.
解答 解:(1)∵直线y=$\frac{1}{2}$x-2交x轴、y轴于点B、C两点,
∴B(4,0),C(0,-2),
∵y=ax2-$\frac{3}{2}$x+c经过点B,C,
∴$\left\{\begin{array}{l}{16a-6+c=0}\\{c=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{c=-2}\end{array}\right.$,
∴y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2;
(2)∵令$\frac{1}{2}$x2-$\frac{3}{2}$x-2=0,解得:x1=-1,x2=4,
∴OA=1,OB=4.
∴AB=5.
∴AC2=OA2+0C2=5,BC2=OC2+OB2=20,AB2=25.
∴AC2+BC2=AB2.
∴△ABC为直角三角形.
(3)如图1所示:连接CD、BD,过点P作PE⊥AB,垂足为E,直线EP交线段BC与点D.
设直线BC的解析式为y=kx+b.
∵将B(4,0),C(0,-2)代入得:$\left\{\begin{array}{l}{b=-2}\\{4k+b=0}\end{array}\right.$,解得:k=$\frac{1}{2}$,b=-2,
∴直线BC的解析式为y=$\frac{1}{2}x-2$.
设点D(a,$\frac{1}{2}a-2$),则点P(a,$\frac{1}{2}$a2-$\frac{3}{2}$a-2).
∵PD=PE-DE=-$\frac{1}{2}$a2+$\frac{3}{2}$a+2+($\frac{1}{2}a$-2)=-$\frac{1}{2}$a2+2a,
∴当a=2时,PD有最大值,PD的最大值=2.
∵四边形ACPB的面积=S△ACB+S△CBP=$\frac{1}{2}AB•OC$+$\frac{1}{2}OB•DP$=$\frac{1}{2}$×5×2+$\frac{1}{2}$×4×DP=5+2PD.
∴当PD最大时,四边形ACPB的面积最大.
∴当P的坐标为(2,-3)时,四边形ACPB的面积的最大值=5+2×2=9.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、勾股定理、勾股定理的逆定理、三角形的面积公式、二次函数的图象和性质,列出四边形PD与a的函数关系式是解题的关键.

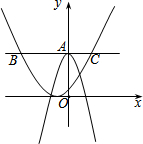 如图,在平面直角坐标系中,过点A与x轴平行的直线交抛物线y=$\frac{1}{3}{(x+1)^2}$于点B、C,线段BC的长度为6,抛物线y=-2x2+b与y轴交于点A,则b=( )
如图,在平面直角坐标系中,过点A与x轴平行的直线交抛物线y=$\frac{1}{3}{(x+1)^2}$于点B、C,线段BC的长度为6,抛物线y=-2x2+b与y轴交于点A,则b=( )| A. | 1 | B. | 4.5 | C. | 3 | D. | 6 |
| 次数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数 | 1 | 8 | 10 | 7 | 6 | 6 | 6 | 4 | 1 | 2 | 0 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
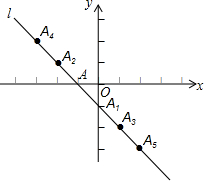 如图在平面直角坐标系xOy中,直线l经过点 A(-1,0),点 A1,A2,A3,A4,A5,…按所示的规律排列在直线l上.若直线l上任意相邻两个点的横坐标都相差1、纵坐标也都相差1,若点An(n为正整数)的横坐标为2015,则n=4031.
如图在平面直角坐标系xOy中,直线l经过点 A(-1,0),点 A1,A2,A3,A4,A5,…按所示的规律排列在直线l上.若直线l上任意相邻两个点的横坐标都相差1、纵坐标也都相差1,若点An(n为正整数)的横坐标为2015,则n=4031. 在三角形ABC中,∠C=90°,AC=5,BC=12,AB=13.则点B到AC的距离是12.
在三角形ABC中,∠C=90°,AC=5,BC=12,AB=13.则点B到AC的距离是12.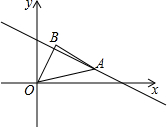 如图,点A是直线y=-$\frac{1}{2}$x+3在第一象限内的一点;连接OA,以OA为斜边向上作等腰直角三角形OAB,若点A的横坐标为4,则点B的坐标为($\frac{3}{2}$,$\frac{5}{2}$).
如图,点A是直线y=-$\frac{1}{2}$x+3在第一象限内的一点;连接OA,以OA为斜边向上作等腰直角三角形OAB,若点A的横坐标为4,则点B的坐标为($\frac{3}{2}$,$\frac{5}{2}$). 如图,长方形的长为(a+b),宽为(a-b),圆的半径为$\frac{1}{2}a$,求阴影部分的面积(π取3.14).
如图,长方形的长为(a+b),宽为(a-b),圆的半径为$\frac{1}{2}a$,求阴影部分的面积(π取3.14).