题目内容
1.王老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:优秀;B:良好;C:合格;D:一般;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题: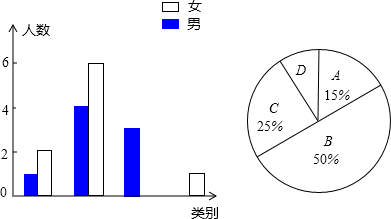
(1)本次调查中,王老师一共调查了20名同学,其中C类女生有2名,D类男生有1名;
(2)将上面的条形统计图补充完整;
(3)从被调查的A类和D类学生中分别选取一位同学进行“一对一”互助学习,请求出所选两位同学恰好是一位男同学和一位女同学的概率.
分析 (1)由条形统计图与扇形统计图,即可求得调查的总人数,继而分别求得C类女生与D类男生数;
(2)由(1)可补全条形统计图;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所选两位同学恰好是一位男同学和一位女同学的情况,再利用概率公式即可求得答案.
解答 解:(1)本次调查中,王老师一共调查了:(4+6)÷50%=20(名);
其中C类女生有:20×25%-3=2(名),D类男生有:20-1-2-4-6-3-2-1=1(名);
故答案为:20,2,1;
(2)如图: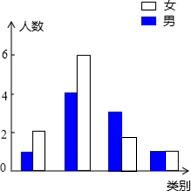
(3)画树状图得: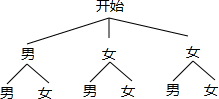
∵共有6种等可能的结果,所选两位同学恰好是一位男同学和一位女同学的有3种情况,
∴所选两位同学恰好是一位男同学和一位女同学的概率为:$\frac{3}{6}$=$\frac{1}{2}$.
点评 此题考查了列表法或树状图法求概率以及条形统计图与扇形统计图的知识.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
12.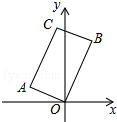 如图,在矩形AOBC中,点A的坐标(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
 如图,在矩形AOBC中,点A的坐标(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )| A. | ($\frac{7}{4}$,$\frac{7}{2}$)、(-$\frac{1}{2}$,4) | B. | ($\frac{3}{2}$,3)、(-$\frac{2}{3}$,4) | C. | ($\frac{3}{2}$,3)、(-$\frac{1}{2}$,4) | D. | ($\frac{7}{4}$,$\frac{7}{2}$)、(-$\frac{2}{3}$,4) |
16.表示两个变量之间的关系,下列说法错误的是( )
| A. | 用表格可以表示任意两个变量之间的关系 | |
| B. | 用关系式可以表示任意两个变量之间的关系 | |
| C. | 用图象可以表示任意两个变量之间的关系 | |
| D. | 在某一变化过程中,数值始终不变的量叫常量 |
6.某校从各年级随机抽取50名学生,每人进行10次投篮,投篮进球次数如下表所示:该投篮进球数据的中位数是( )
| 次数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数 | 1 | 8 | 10 | 7 | 6 | 6 | 6 | 4 | 1 | 2 | 0 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
10.将∠AOB绕点O顺时针旋转15°,得到∠COD,若∠COD=45°,则∠AOB的度数是( )
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
11.下列计算结果正确的是( )
| A. | a4•a2=a8 | B. | (a4)2=a6 | C. | (ab)2=a2b2 | D. | (a-b)2=a2-b2 |
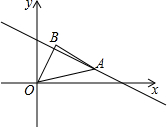 如图,点A是直线y=-$\frac{1}{2}$x+3在第一象限内的一点;连接OA,以OA为斜边向上作等腰直角三角形OAB,若点A的横坐标为4,则点B的坐标为($\frac{3}{2}$,$\frac{5}{2}$).
如图,点A是直线y=-$\frac{1}{2}$x+3在第一象限内的一点;连接OA,以OA为斜边向上作等腰直角三角形OAB,若点A的横坐标为4,则点B的坐标为($\frac{3}{2}$,$\frac{5}{2}$).