题目内容
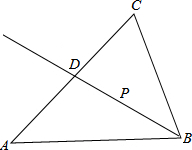 如图已知,在△ABC中,∠A=60°,BD是∠ABC的平分线.
如图已知,在△ABC中,∠A=60°,BD是∠ABC的平分线.(1)求∠ABD+
| 1 |
| 2 |
(2)P为射线BD上一动点,当点P在线段BD上时,连接PC,请猜想PB+PC与AB+AC的大小关系,并证明你的猜想;
(3)当点P在射线BD上运动时,是否存在一点P,使∠BPC=30°?若存在,请比较∠ACP和∠ABD的度数的大小关系,若不存在请说明理由.
考点:三角形内角和定理,三角形的外角性质
专题:探究型
分析:(1)由角平分线的定义可得∠ABD+
∠ACB=
∠ABC+
∠ACB,再利用三角形内角和定理求出∠ABC+∠ACB即可;
(2)连接PC,在△ABD和△PDC中分别利用三角形三边之间的关系即可得出结论;
(3)在△ABD和△CPD中分别利用内角和定理,可得出∠ABD+∠A=∠ACP+∠BPC,再把角的度数代入可求得结论.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)连接PC,在△ABD和△PDC中分别利用三角形三边之间的关系即可得出结论;
(3)在△ABD和△CPD中分别利用内角和定理,可得出∠ABD+∠A=∠ACP+∠BPC,再把角的度数代入可求得结论.
解答:解:
(1)∵BD是∠ABC的平分线,
∴∠ABD=
∠ABC,
∴∠ABD+
∠ACB=
∠ABC+
∠ACB=
(∠ABC+∠ACB)=
(180°-∠A)=
×120°=60°;
(2)AB+AC>PB+PC,证明如下:
如图,连接PC,

在△ABD中,有AB+AD>BD,即AB+AD>PB+PD,
在△PDC中,有PD+DC>PC,
∴AB+AD+PD+DC>PB+PD+PC,
∴AB+AD+DC>PB+PC,
即AB+AC>PB+PC;
(3)存在,∠ABD<∠ACP,理由如下:
∠BPC=30°,则点P的BD的延长线上,
则∠ABD+∠A+∠ADB=∠ACP+∠BPC+∠CDP=180°,
∵∠ADB=∠CDP,
∴∠ABD+∠A=∠ACP+∠BPC,
即∠ABD+60°=∠ACP+30°,
∴∠ABD+30°=∠ACP,
∴∠ABD<∠ACP.
(1)∵BD是∠ABC的平分线,
∴∠ABD=
| 1 |
| 2 |
∴∠ABD+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)AB+AC>PB+PC,证明如下:
如图,连接PC,

在△ABD中,有AB+AD>BD,即AB+AD>PB+PD,
在△PDC中,有PD+DC>PC,
∴AB+AD+PD+DC>PB+PD+PC,
∴AB+AD+DC>PB+PC,
即AB+AC>PB+PC;
(3)存在,∠ABD<∠ACP,理由如下:
∠BPC=30°,则点P的BD的延长线上,
则∠ABD+∠A+∠ADB=∠ACP+∠BPC+∠CDP=180°,
∵∠ADB=∠CDP,
∴∠ABD+∠A=∠ACP+∠BPC,
即∠ABD+60°=∠ACP+30°,
∴∠ABD+30°=∠ACP,
∴∠ABD<∠ACP.
点评:本题主要考查三角形内角和定理及角平分线、三角形的三边关系,在复杂图形中能找到所需要的三角形中找到角之间的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在一幅长为60cm,宽为40cm的矩形风景画的四周镶一条相同宽度的纸边,制成一幅矩形挂图.若要使整个挂图的面积是3500cm2,设纸边的宽为x(cm),则x满足的方程是( )
如图,在一幅长为60cm,宽为40cm的矩形风景画的四周镶一条相同宽度的纸边,制成一幅矩形挂图.若要使整个挂图的面积是3500cm2,设纸边的宽为x(cm),则x满足的方程是( )| A、(60+x)(40+x)=3500 |
| B、(60+2x)(40+2x)=3500 |
| C、(60-x)(40-x)=3500 |
| D、(60-2x)(40-2x)=3500 |
 在四边形ABCD中,AD∥BC,BD是∠ABC的平分线,且CD⊥BD,AD=4,CD=2.
在四边形ABCD中,AD∥BC,BD是∠ABC的平分线,且CD⊥BD,AD=4,CD=2. 如图,在△ABC中,∠C=90°,∠A=30°,试通过折叠法证明∠A的对边BC是斜边AB的一半.
如图,在△ABC中,∠C=90°,∠A=30°,试通过折叠法证明∠A的对边BC是斜边AB的一半. 如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点.
如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点.