题目内容
 在四边形ABCD中,AD∥BC,BD是∠ABC的平分线,且CD⊥BD,AD=4,CD=2.
在四边形ABCD中,AD∥BC,BD是∠ABC的平分线,且CD⊥BD,AD=4,CD=2.(1)求sin∠ABD;
(2)求S四边形ABCD.
考点:解直角三角形
专题:计算题
分析:(1)延长CD,交BA的延长线于E,如图,由于BD是∠ABC的平分线,CD⊥BD,根据等腰三角形的判定方法得到△BCE为等腰三角形,则CD=ED=2,∠C=∠E,BE=BC,再判断AD为△EBC的中位线得到BC=2AD=8,即BE=8,然后在Rt△BDE中根据正弦的定义求解;
(2)作DF⊥BC于F,如图,在Rt△BDC中,利用勾股定理计算出BD=2
,再利用面积法计算出DF,然后根据梯形的面积公式求解.
(2)作DF⊥BC于F,如图,在Rt△BDC中,利用勾股定理计算出BD=2
| 15 |
解答:解:(1)延长CD,交BA的延长线于E,如图,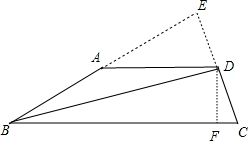
∵BD是∠ABC的平分线,CD⊥BD,
∴△BCE为等腰三角形,CD=ED=2,
∴∠C=∠E,BE=BC,
∵AD∥BC,
∴AD为△EBC的中位线,
∴BC=2AD=8,
∴BE=8,
在Rt△BDE中,sin∠EBD=
=
=
;
即sin∠ABD=
;
(2)作DF⊥BC于F,如图,
在Rt△BDC中,
∵CD=2,BC=8,
∴BD=
=2
,
∵
BD•CD=
BC•DF,
∴DF=
=
,
∴S四边形ABCD=
•(4+8)•
=3
.

∵BD是∠ABC的平分线,CD⊥BD,
∴△BCE为等腰三角形,CD=ED=2,
∴∠C=∠E,BE=BC,
∵AD∥BC,
∴AD为△EBC的中位线,
∴BC=2AD=8,
∴BE=8,
在Rt△BDE中,sin∠EBD=
| DE |
| AE |
| 2 |
| 8 |
| 1 |
| 4 |
即sin∠ABD=
| 1 |
| 4 |
(2)作DF⊥BC于F,如图,
在Rt△BDC中,
∵CD=2,BC=8,
∴BD=
| BC2-CD2 |
| 15 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴DF=
2×2
| ||
| 8 |
| ||
| 2 |
∴S四边形ABCD=
| 1 |
| 2 |
| ||
| 2 |
| 15 |
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了等腰三角形的判定与性质.

练习册系列答案
相关题目
 如图,直角三角形ABC中,∠C=90°,D为AC上一点,DA=DB=5,△ABD的面积为10,则CD长是( )
如图,直角三角形ABC中,∠C=90°,D为AC上一点,DA=DB=5,△ABD的面积为10,则CD长是( )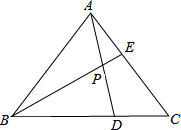 已知如图,在△ABC的边BC,AC上分别取点D、E,使BD=2CD,CE=2AE,AD与BE的交点为P,求证:S△EPA:S△APB:S△BPD:S△ABC=1:6:8:21.
已知如图,在△ABC的边BC,AC上分别取点D、E,使BD=2CD,CE=2AE,AD与BE的交点为P,求证:S△EPA:S△APB:S△BPD:S△ABC=1:6:8:21.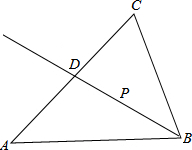 如图已知,在△ABC中,∠A=60°,BD是∠ABC的平分线.
如图已知,在△ABC中,∠A=60°,BD是∠ABC的平分线.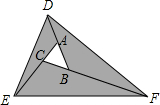 如图,已知△ABC,现将边BA延长至点D,使AD=AB,延长AC至点E,使CE=2AC.延长CB至点F,使BF=3BC,分别连结DE,DF,EF,得到△DEF,若△ABC的面积为1,则阴影部分的面积为
如图,已知△ABC,现将边BA延长至点D,使AD=AB,延长AC至点E,使CE=2AC.延长CB至点F,使BF=3BC,分别连结DE,DF,EF,得到△DEF,若△ABC的面积为1,则阴影部分的面积为