题目内容
设一列数1、
、
、
、…、
的和为Sn,则Sn= .
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n-1 |
考点:规律型:数字的变化类
专题:
分析:由已知Sn=1+
+
+
+…+
,将这个等式两边同时乘以
,得:
Sn=
+
+
+…+
,然后两式相减,得:
Sn=1-
,进而得到:Sn=2-
.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 2n |
| 1 |
| 2n-1 |
解答:解:∵Sn=1+
+
+
+…+
①,
∴
Sn=
+
+
+…+
②,
∴①-②得:
Sn=1-
,
∴Sn=2-
.
故答案为:2-
.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n-1 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
∴①-②得:
| 1 |
| 2 |
| 1 |
| 2n |
∴Sn=2-
| 1 |
| 2n-1 |
故答案为:2-
| 1 |
| 2n-1 |
点评:此题考查了数字的变化类的规律型题,解题的关键是:表示
Sn=
+
+
+…+
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
甲型H1N1流感病毒是A型流感病毒,携带有H1N1亚型猪流感病毒毒株,包含有禽流感、猪流感和人流感三种流感病毒,预计今年全球将有约三千万人感染该病毒的危险.请用科学记数法表示:三千万( )
| A、3×106 |
| B、3×107 |
| C、3×108 |
| D、3×109 |
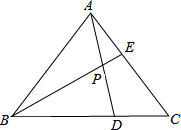 已知如图,在△ABC的边BC,AC上分别取点D、E,使BD=2CD,CE=2AE,AD与BE的交点为P,求证:S△EPA:S△APB:S△BPD:S△ABC=1:6:8:21.
已知如图,在△ABC的边BC,AC上分别取点D、E,使BD=2CD,CE=2AE,AD与BE的交点为P,求证:S△EPA:S△APB:S△BPD:S△ABC=1:6:8:21. 如图已知,在△ABC中,∠A=60°,BD是∠ABC的平分线.
如图已知,在△ABC中,∠A=60°,BD是∠ABC的平分线. 如图,在△ABC中,DE∥FG∥BC,AD:DF:BF=1:2:3,BC=10cm.
如图,在△ABC中,DE∥FG∥BC,AD:DF:BF=1:2:3,BC=10cm.