题目内容
18. 如图,过⊙O外一点P作⊙O的两条切线,切点分别为A、B,点M是劣弧$\widehat{AB}$上的任一点,过M作⊙0的切线分别交PA、PB于点C、D,过圆心O且垂直于OP的直线与PA、PB分别交于点E、F,那么$\frac{EC•FD}{E{F}^{2}}$的值为( )
如图,过⊙O外一点P作⊙O的两条切线,切点分别为A、B,点M是劣弧$\widehat{AB}$上的任一点,过M作⊙0的切线分别交PA、PB于点C、D,过圆心O且垂直于OP的直线与PA、PB分别交于点E、F,那么$\frac{EC•FD}{E{F}^{2}}$的值为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
分析 先证明△EOC∽△FDO,由此得到EC•FD=EO2,即可得到答案.
解答 解:∵PA、PB、CD都是⊙O的切线,
∴∠OPE=∠OPF,∠OAC=∠OCD,∠ODM=∠ODB,OA⊥PE,OM⊥CD,OB⊥PF,
∴∠OAC=∠OMC=∠OMD=∠OBD=90°,
∵∠COA+∠AOC=90°,∠OCD+∠COM=90°∴∠COA=∠COM,
同理∠DOM=∠DOB,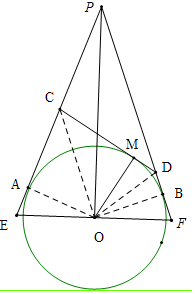
∵PO⊥EF,
∴∠OPE=∠POF=90°,
∴∠OPE+∠E=90°,∠OPF+∠F=90°,
∴∠E=∠F,
∴PE=PF,∵∠EPO=∠FPO,
∴OE=OF,
∵∠E+∠AOE=90°,∠F+∠FOB=90°,
∴∠AOE=∠BOF,
∵∠AOE+∠AOC+∠COM+∠MOD+∠DOB+∠FOB=180°,
∴2∠BOF+2∠AOC+2∠DOB=180°,
∴∠BOF+∠AOC+∠DOB=90°,
∴∠AOC+∠DOF=90°,∵∠AOC+∠ACO=90°,
∴∠ACO=∠DOF,∵∠E=∠F,
∴△EOC∽△FDO,
∴$\frac{EO}{DF}$=$\frac{EC}{FO}$,
∴EC•DF=OE•OF=OE2,
∴$\frac{EC•DF}{E{F}^{2}}$=$\frac{O{E}^{2}}{4O{E}^{2}}$=$\frac{1}{4}$.
故选A.
点评 本题考查切线的性质、相似三角形的判定和性质、确定哪两个三角形相似是解决本题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
8. 如图,四边形ABCD为正方形,边长为4,点F在AB边上,E为射线AD上一点,正方形ABCD沿直线EF折叠,点A落在G处,已知点G恰好在以AB为直径的圆上,则CG的最小值等于( )
如图,四边形ABCD为正方形,边长为4,点F在AB边上,E为射线AD上一点,正方形ABCD沿直线EF折叠,点A落在G处,已知点G恰好在以AB为直径的圆上,则CG的最小值等于( )
 如图,四边形ABCD为正方形,边长为4,点F在AB边上,E为射线AD上一点,正方形ABCD沿直线EF折叠,点A落在G处,已知点G恰好在以AB为直径的圆上,则CG的最小值等于( )
如图,四边形ABCD为正方形,边长为4,点F在AB边上,E为射线AD上一点,正方形ABCD沿直线EF折叠,点A落在G处,已知点G恰好在以AB为直径的圆上,则CG的最小值等于( )| A. | 0 | B. | 2$\sqrt{5}$ | C. | 4-2$\sqrt{5}$ | D. | 2$\sqrt{5}$-2 |
13.某学校组织了一次知识竞赛,初二年级、初三年级各10名选手的比赛成绩如下(本次竞赛满分10分):
(1)初二成绩的中位数是9.5分,初三成绩的众数是10分;
(2)运用学过的数学知识说明、判断,哪个年级选手的成绩整体比较稳定.
| 初二 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 初三 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(2)运用学过的数学知识说明、判断,哪个年级选手的成绩整体比较稳定.
 如图,等边△ABC的边长为4,AD是BC边上的中线,M是AD上的动点,E是AC边上点,若AE=1,EM+CM的最小值为$\sqrt{13}$.
如图,等边△ABC的边长为4,AD是BC边上的中线,M是AD上的动点,E是AC边上点,若AE=1,EM+CM的最小值为$\sqrt{13}$. 如图.在?ABCD中,点E、F为对角线AC上的三等分点,求证:四边形BFDE是平行四边形.
如图.在?ABCD中,点E、F为对角线AC上的三等分点,求证:四边形BFDE是平行四边形. AB是⊙O的直径,弦CD垂直平分半径OA,若CD长为6,则⊙O的半径长为2$\sqrt{3}$.
AB是⊙O的直径,弦CD垂直平分半径OA,若CD长为6,则⊙O的半径长为2$\sqrt{3}$.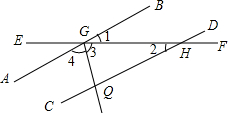 如图,直线AB,CD被直线EF所截,∠AGH的平分线交CD于点Q,已知∠1=∠2=$\frac{1}{4}$∠3,求∠1,∠3的度数.
如图,直线AB,CD被直线EF所截,∠AGH的平分线交CD于点Q,已知∠1=∠2=$\frac{1}{4}$∠3,求∠1,∠3的度数. 如图,AB⊥CD于点B,AE与BF相交于点G,且∠FGE=60°,∠ABG=30°.判断AE与CD是否平行,并说明理由.
如图,AB⊥CD于点B,AE与BF相交于点G,且∠FGE=60°,∠ABG=30°.判断AE与CD是否平行,并说明理由.