题目内容
16.化简:($\frac{a-2}{{a}^{2}+2a}$$-\frac{1}{a+2}$)÷$\frac{2}{a+2}$.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:原式=$\frac{a-2-a}{a(a+2)}$•$\frac{a+2}{2}$
=-$\frac{2}{a(a+2)}$•$\frac{a+2}{2}$
=-$\frac{1}{a}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
6.若直角三角形两条直角边的长分别为6和8,则斜边上的中线是( )
| A. | 5 | B. | 10 | C. | $\frac{24}{5}$ | D. | $\frac{12}{5}$ |
1.点P在第三象限,该点到x轴的距为$\sqrt{2}$,到y轴的距离为2,则点P的坐标为( )
| A. | (-$\sqrt{2}$,-2) | B. | (-2,-$\sqrt{2}$) | C. | (-2,$\sqrt{2}$) | D. | (2,$\sqrt{2}$) |
5.下列等式成立的是( )
| A. | $\frac{0.1a}{0.1a-b}$=$\frac{a}{a-b}$ | B. | $\frac{-a}{a-b}$=$\frac{a}{a+b}$ | C. | $\frac{a}{a+b}$=$\frac{1}{b}$ | D. | $\frac{a}{b}$=$\frac{ab}{{b}^{2}}$ |
6.已知(x+m)2=x2+nx+36,则n的值为( )
| A. | ±6 | B. | ±12 | C. | ±18 | D. | ±72 |
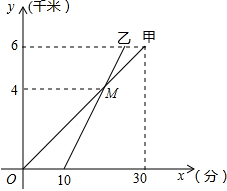 已知A、B两地的路程是6千米.甲骑自行车、乙骑摩托车,他们沿相同路线由A地到B地走完全程,甲、乙行驶过程中的路程随时间变化的函数关系的图象如图所示,根据图象解决下列问题:
已知A、B两地的路程是6千米.甲骑自行车、乙骑摩托车,他们沿相同路线由A地到B地走完全程,甲、乙行驶过程中的路程随时间变化的函数关系的图象如图所示,根据图象解决下列问题: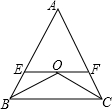 如图,△ABC中,BO平分∠ABC,CO平分∠ACB,EF∥BC,EF经过点O,若AB=10,AC=15,则△AEF的周长是( )
如图,△ABC中,BO平分∠ABC,CO平分∠ACB,EF∥BC,EF经过点O,若AB=10,AC=15,则△AEF的周长是( )