题目内容
6．若直角三角形两条直角边的长分别为6和8，则斜边上的中线是（ ）| A． | 5 | B． | 10 | C． | $\frac{24}{5}$ | D． | $\frac{12}{5}$ |
分析 直接利用勾股定理得出其斜边长，再利用直角三角形的性质得出其中线的长．
解答 解：∵直角三角形两条直角边的长分别为6和8，
∴直角三角形的斜边长为：$\sqrt{{6}^{2}+{8}^{2}}$=10，
则斜边上的中线是：10×$\frac{1}{2}$=5（直角三角形斜边上的中线等于斜边的一半）．
故选：A．
点评 此题主要考查了勾股定理以及直角三角形的性质，正确掌握直角三角形斜边的中线等于斜边的一半是解题关键．
练习册系列答案
相关题目
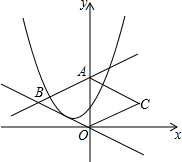如图，直线y=$\frac{1}{2}$x+2交y轴于点A，与直线y=-$\frac{1}{2}$x交于点B，把△AOB沿y轴翻折，得到△AOC，
如图，点B、E分别在AC、DF上，AF分别交BD、CE于点M、N，∠1=∠2，∠C=∠D．
1．a，b都是实数，且a＜b，则下列不等式的变形正确的是（ ）
| A． | a+x＞b+x | B． | -a+1＜-b+1 | C． | 2a＜2b | D． | $\frac{a}{2}$＞$\frac{b}{2}$ |
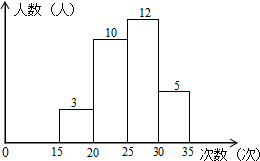某学校为了了解八年级学生的体能情况，随机选取30名学生测试一分钟仰卧起坐次数，并绘制了如图的直方图，学生仰卧起坐次数在15～20之间的频率为0.1．